
科目:gzsx 来源: 题型:
| 1 |
| 2n+1 |
| an |
| 2n+1 |
| an |
| 2n+1 |
科目:gzsx 来源: 题型:
| an+1 |
| an |
| an+1 |
| an |
| an |
| an-1 |
| a1 |
| 3! |
| a2 |
| 4! |
| a3 |
| 5! |
| an |
| (n+2)! |
科目:gzsx 来源:2007年上海市徐汇区零陵中学高三3月综合练习数学试卷(三)(解析版) 题型:解答题
 在曲线C上,并有a1=1,
在曲线C上,并有a1=1, .
. ,对于一切n∈N*,都有Sn>m成立,求自然数m的最大值.
,对于一切n∈N*,都有Sn>m成立,求自然数m的最大值.科目:gzsx 来源: 题型:
其中°F函数的序号为_____________.
科目:gzsx 来源:2010年上海市上海中学高三数学综合练习试卷(9)(解析版) 题型:解答题
 在曲线C上,并有a1=1,
在曲线C上,并有a1=1, .
. ,对于一切n∈N*,都有Sn>m成立,求自然数m的最大值.
,对于一切n∈N*,都有Sn>m成立,求自然数m的最大值.科目:gzsx 来源:不详 题型:解答题
| 1 |
| 2n+1 |
| an |
| 2n+1 |
| an |
| 2n+1 |
科目:gzsx 来源:2008-2009学年高三(上)数学寒假作业(文科)(解析版) 题型:解答题
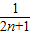 ,
, ,试判断并说明cn+1-cn(n∈N*)的符号;
,试判断并说明cn+1-cn(n∈N*)的符号; ,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.
,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.科目:gzsx 来源:2008-2009学年高三(上)数学寒假作业(理科)(解析版) 题型:解答题
 ,
, ,试判断并说明cn+1-cn(n∈N*)的符号;
,试判断并说明cn+1-cn(n∈N*)的符号; ,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.
,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.科目:gzsx 来源:2010年江西省九江市都昌二中高考数学模拟试卷(文科)(解析版) 题型:解答题
 ,
, ,试判断并说明cn+1-cn(n∈N*)的符号;
,试判断并说明cn+1-cn(n∈N*)的符号; ,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.
,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.科目:gzsx 来源: 题型:解答题
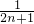 ,
,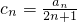 ,试判断并说明cn+1-cn(n∈N*)的符号;
,试判断并说明cn+1-cn(n∈N*)的符号;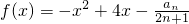 ,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.
,是否存在最大的实数λ,当x≤λ时,对于一切自然数n,都有f(x)≤0.科目:gzsx 来源:江苏省常州二中2008高考一轮复习综合测试4、数学(文科) 题型:044
已知数列{an}及{bn}其中a1=1,an=2nbn,an+1-2an=2n.
(1)求证{bn}成等差数列;
(2)求数列{an}的通项公式;
(3)若函数f(x)=-x2+4x-![]() 对于一切正整数n都有f(x)≤0,求x的取值范围.
对于一切正整数n都有f(x)≤0,求x的取值范围.
科目:gzsx 来源:新课程高中数学疑难全解 题型:044
已知二次函数f(x)=2x2-4(a-1)x-a2+2a+9.
(1)若在区间[-1,1]内至少存在一个实数m,使得f(m)>0,求实数a的取值范围;
(2)若在区间[-1,1]内的一切实数m,都有f(m)>0,求实数a的取值范围.
科目:gzsx 来源:2014届福建省高二下学期5月月考文科数学卷(解析版) 题型:选择题
如果函数f(x)=x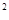 +bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么( )
A.f(2)<f(1)<f(4) B.f(1)<f(2)<f(4)
C.f(2)<f(4)<f(1) D.f(4)<f(2)<f(1)
科目:gzsx 来源: 题型:022
下列四个命题:
(1)若函数满足f(x-a)=f(a-x),则f(x)的图象关于y轴对称
(2)若函数f(x)满足f(x-a)=f(a-x),则函数f(x)的图象关于直线x=a对称
(3)函数y=f(x+a)与y=f(a-x)的图象关于y轴对称
(4)函数y=f(x+a)与y=f(a-x)的图象关于直线x=a对称
其中正确的命题是________.
科目:gzsx 来源: 题型:013
(2007
黄冈模拟)若函数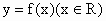 满足f(x+2)=f(x),且
满足f(x+2)=f(x),且 时
时 ,则函数y=f(x)的图象与函数y=1g
,则函数y=f(x)的图象与函数y=1g 的图象的交点个数为
的图象的交点个数为
[
]|
A .16 |
B .18 |
C .20 |
D .无数个 |
科目:gzsx 来源:浙江省金华一中2011-2012学年高二下学期期中考试数学文科试题 题型:013
已知y=f(x)是R上的可导函数,对任意的正实数t,都有g(x)=f(x+t)-f(x)在其定义域内为增函数,则函数y=![]() (x)的图像可能是
(x)的图像可能是
A.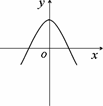
B.
C.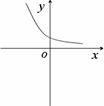
D.
科目:gzsx 来源:101网校同步练习 高三数学 苏教版(新课标·2004年初审) 苏教版 题型:013
如果函数f(x)=x2+bx+c对于任意实数t,都有f(2+t)=f(2-t),那么
A.f(2)<f(1)<f(4)
B.f(1)<f(2)<f(4)
C.f(2)<f(4)<f(1)
D.f(4)<f(2)<f(1)