科目：czsx 来源：同步题 题型：证明题

已知：如图，AB=DC，AD=BC，O是DB的中点，过O点的直线分别交DA和BC的延长线于E，F．
求证：∠E=∠F．

科目：czsx 来源： 题型：

21、已知，如图，AB=DC，AD=BC，试问：∠B与∠D相等吗？请你说明理由．

科目：czsx 来源： 题型：

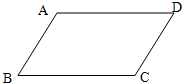21、已知：如图，AB∥DC，AD∥BC，求证：∠A=∠C．               
（补充下列证明）
证明：∵AB∥DC     （  已知  ）
∴∠A+∠D=180°

（两直线平行，同旁内角互补）

∵AD∥BC

（ 已知 ）

∴

∠A+∠C=180°

∴

∠A=∠C

．

科目：czsx 来源：不详 题型：解答题

已知：如图，AB∥DC，AD∥BC，求证：∠A=∠C．               
（补充下列证明）
证明：∵AB∥DC     （  已知  ）
∴∠A+∠D=180°______
∵AD∥BC______
∴______
∴______．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：解答题

科目：czsx 来源： 题型：填空题

科目：czsx 来源： 题型：

24、已知：如图，AB=AC，AD⊥BC，垂足是F，P是AD上任意的一点，求证：PB=PC．

科目：czsx 来源：同步题 题型：证明题

已知：如图，AB=AC，AD⊥BC，垂足是F，P是AD上任意的一点，求证：PB=PC．

科目：czsx 来源： 题型：解答题

科目：czsx 来源： 题型：

已知：如图，AB∥CD，AD∥BC，∠1=50°，∠2=80°．求∠C的度数．

科目：czsx 来源： 题型：

28、已知：如图，AB=AC，AD⊥BC于D，DF∥AE．求证：CE=2DF．

科目：czsx 来源： 题型：

已知：如图，AB=AC，AD⊥BC于D，EC⊥BC，BE交AD于F，交AC于G且AD=BC=2CE．
求证：（1）△ADC≌△BCE；（2）BE⊥AC．

科目：czsx 来源： 题型：

22、已知：如图，AB∥CD，AD∥BC．求证：∠A=∠C．
证明：∵AB∥CD，（

已知

）
∴∠B+∠C=180°．（

两直线平行，同旁内角互补

）
∵AD∥BC，（已知）
∴∠A+∠B=180°．（

两直线平行，同旁内角互补

）
∴∠A=∠C．（

等量代换

）

科目：czsx 来源：2013届浙江省八年级下学期期中数学试卷（解析版） 题型：解答题

科目：czsx 来源：2011-2012学年浙江省温州四中八年级下学期期中数学试卷（带解析） 题型：解答题

科目：czsx 来源：101网校同步练习　初二数学　北师大(新课标2001/3年初审) 北师大(新课标2001/3年初审) 题型：044

已知：如图，AB∥CD，AD∥BC，∠1＝50°，∠2＝80°．

求：∠C的度数．

科目：czsx 来源：北京期中题 题型：解答题

已知：如图，AB=AC，AD⊥BC于D，DF∥AE。求证：CE=2DF。

科目：czsx 来源： 题型：解答题

科目：czsx 来源：同步题 题型：证明题

已知：如图，AB=CD，AD=BC，AO=OC，EF过O点．求证：OE=OF．