二次函数的图像的顶点在原点,且过点(2,4),求这个二次函数的关系式答案解析
科目:czsx
来源:学习周报 数学 北师大九年级版 2009-2010学年 第17期 总第173期 北师大版
题型:044
已知抛物线的顶点在原点,且过点(3,-27),求抛物线的函数表达式.
查看答案和解析>>
科目:czsx
来源:
题型:
20、根据下列条件求抛物线的解析式:
(1)已知抛物线的顶点在原点,且过点(3,18);
(2)已知抛物线的顶点坐标为(-1,-2),且过点(0,-3).
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
根据下列条件求抛物线的解析式:
(1)已知抛物线的顶点在原点,且过点(3,18);
(2)已知抛物线的顶点坐标为(-1,-2),且过点(0,-3).
查看答案和解析>>
科目:czsx
来源:2009-2010学年福建省厦门市上塘中学九年级(上)期中数学试卷(解析版)
题型:解答题
根据下列条件求抛物线的解析式:
(1)已知抛物线的顶点在原点,且过点(3,18);
(2)已知抛物线的顶点坐标为(-1,-2),且过点(0,-3).
查看答案和解析>>
科目:czsx
来源:
题型:解答题
根据下列条件求抛物线的解析式:
(1)已知抛物线的顶点在原点,且过点(3,18);
(2)已知抛物线的顶点坐标为(-1,-2),且过点(0,-3).
查看答案和解析>>
科目:czsx
来源:上海市期末题
题型:填空题
若某二次函数图像的顶点在原点,且经过点(2,1),则此二次函数的解析式是( )。
查看答案和解析>>
科目:czsx
来源:
题型:
若某二次函数图象的顶点在原点,且经过点(2,1),则此二次函数的解析式是
.
查看答案和解析>>
科目:czsx
来源:2010年上海市卢湾区中考数学一模试卷(解析版)
题型:填空题
(2010•卢湾区一模)若某二次函数图象的顶点在原点,且经过点(2,1),则此二次函数的解析式是 .
查看答案和解析>>
科目:czsx
来源:
题型:填空题
若某二次函数图象的顶点在原点,且经过点(2,1),则此二次函数的解析式是________.
查看答案和解析>>
科目:czsx
来源:
题型:
一条抛物线以y轴为对称轴,顶点在原点,且过点(3,2),求这条抛物线的解析式.
查看答案和解析>>
科目:czsx
来源:
题型:044
在平面直角坐标系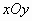 中,已知二次函数
中,已知二次函数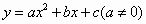 的图象与
的图象与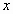 轴交于
轴交于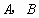 两点(点
两点(点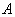 在点
在点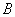 的左边),与
的左边),与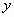 轴交于点
轴交于点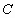 ,其顶点的横坐标为1,且过点
,其顶点的横坐标为1,且过点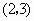 和
和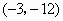 .
.
(1)
求此二次函数的表达式;
(2)
若直线
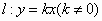
与线段
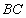
交于点
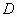 (
(不与点
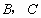
重合
),则是否存在这样的直线
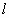
,使得以
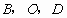
为顶点的三角形与
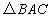
相似?若存在,求出该直线的函数表达式及点
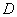
的坐标;若不存在,请说明理由;
(3)
若点
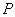
是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角
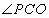
与
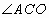
的大小
(不必证明
),并写出此时点
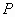
的横坐标
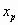
的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y0).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线C:y=x2-(m+1)x+1与x轴只有一个交点.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后,再作关于y轴的轴对称变换得到抛物线C1,并且C1过点(n,3),求C1的函数关系式;
(3)m<0时,抛物线C的顶点为M,且过点P(-2,y0),连接OP,问在抛物线上是否存在一点Q,使以点Q和O、M、P中任意两点构成的三角形与△OPM的面积相等?如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012-2013学年北京市十五中九年级(上)期中数学试卷(解析版)
题型:解答题
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2013年北京市人大附中中考数学冲刺试卷(一)(解析版)
题型:解答题
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年天津市河东区中考数学二模试卷(解析版)
题型:解答题
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2011年北京市石景山区中考数学一模试卷(解析版)
题型:解答题
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y0).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知抛物线C:y=x2-(m+1)x+1与x轴只有一个交点.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后,再作关于y轴的轴对称变换得到抛物线C1,并且C1过点(n,3),求C1的函数关系式;
(3)m<0时,抛物线C的顶点为M,且过点P(-2,y0),连接OP,问在抛物线上是否存在一点Q,使以点Q和O、M、P中任意两点构成的三角形与△OPM的面积相等?如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:北京市石景山区2011年初中毕业暨中考一模数学试题
题型:059
已知抛物线C:y=x2-(m+1)x+1的顶点在坐标轴上.
(1)求m的值;
(2)m>0时,抛物线C向下平移n(n>0)个单位后与抛物线C1:y=ax2+bx+c关于y轴对称,且C1过点(n,3),求C1的函数关系式;
(3)-3<m<0时,抛物线C的顶点为M,且过点P(1,y0).问在直线x=-1上是否存在一点Q使得△QPM的周长最小,如果存在,求出点Q的坐标,如果不存在,请说明理由.
查看答案和解析>>

![]() 中,已知二次函数
中,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,其顶点的横坐标为1,且过点
,其顶点的横坐标为1,且过点![]() 和
和![]() .
.