已知斜棱柱ABCA1B1C1,侧面A1BB1A1和答案解析

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源：数学教研室 题型：013

科目：gzsx 来源： 题型：013

科目：gzsx 来源： 题型：047

科目：gzsx 来源：成功之路·突破重点线·数学（学生用书） 题型：044

科目：gzsx 来源： 题型：

已知直棱柱ABC-A₁B₁C₁中，底面△ABC为等腰直角三角形，AC=BC=2

2

，∠ACB=90°，AA₁=4，E是AB的中点，F是AA₁的中点，
（1）求证A₁B⊥CE；
（2）求C₁F与侧面ABB₁A₁所成角的正切值；
（3）求异面直线A₁B与C₁F所成角．

科目：gzsx 来源： 题型：

如图所示，已知三棱柱ABC-A₁B₁C₁的各棱长均为2，侧棱B₁B与底面ABC所成的角为，且侧面ABB₁A₁垂直于底面ABC．
（1）证明AB⊥CB₁；
（2）求三棱锥B₁-ABC的体积；
（3）求二面角C-AB₁-B的大小．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

（2007•无锡二模）如图，已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD为直角梯形，AB∥CD，AB⊥AD，AB=AD=A₁B=2CD，侧面A₁ADD₁为正方形．
（1）求直线A₁A与底面ABCD所成角的大小；
（2）求二面角C-A₁B-A正切值的大小；
（3）在棱C₁C上是否存在一点P，使得 D₁P∥平面A₁BC，若存在，试说明点P的位置；若不存在，请说明理由．

科目：gzsx 来源： 题型：

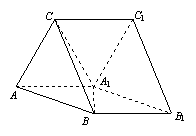
（2013•揭阳二模）如图，已知三棱柱BCF-ADE的侧面CFED与ABFE都是边长为1的正方形，M、N两点分别在AF和CE上，且AM=EN．
（1）求证：平面ABCD⊥平面ADE；
（2）求证：MN∥平面BCF；
（3）若点N为EC的中点，点P为EF上的动点，试求PA+PN的最小值．

科目：gzsx 来源： 题型：

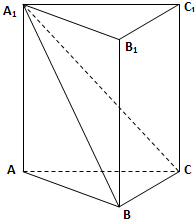
如图，已知三棱柱ABC-A₁B₁C₁中，侧棱A A₁⊥底面ABC，AB⊥BC；
（Ⅰ）求证：平面A₁BC⊥侧面A₁ABB₁．
（Ⅱ）若AA₁=AC=a，直线AC与平面A₁BC所成的角为

π

6

，求AB的长．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

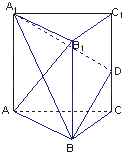
如图，已知三棱柱ABC-A₁B₁C₁的所有棱长都相等，且侧棱垂直于底面，由B沿棱柱侧面经过棱C C₁到点A₁的最短路线长为2

5

，设这条最短路线与CC₁的交点为D．
（1）求三棱柱ABC-A₁B₁C₁的体积；
（2）在平面A₁BD内是否存在过点D的直线与平面ABC平行？证明你的判断；
（3）证明：平面A₁BD⊥平面A₁ABB₁．

科目：gzsx 来源： 题型：

如图，已知三棱柱ABC-A₁B₁C₁的侧棱与底面所成的角为60°，AB=BC，A₁A=A₁C=2，AB⊥BC，侧面AA₁C₁C⊥底面ABC．
（1）证明：A₁B⊥A₁C₁；
（2）求二面角A-CC₁-B的大小；
（3）求经过A₁、A、B、C四点的球的表面积．

科目：gzsx 来源： 题型：

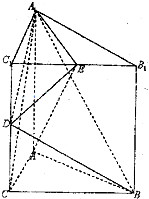
已知三棱柱A₁B₁C₁-ABC中，三个侧面均为矩形，底面ABC为等腰直角三角形，C₁C=CA=CB=2，点D为棱CC₁的中点，点E在棱B₁C₁上运动．
（I）求证A₁C⊥AE；
（II）当点E到达某一位置时，恰使二面角E-A₁D-B的平面角的余弦值为

6

6

，求

C1E

C1B1

；
（III）在（II）的条件下，在平面ABC上确定点F，使得EF⊥平面A₁DB？并求出EF的长度．

科目：gzsx 来源： 题型：

已知三棱柱ABC-A₁B₁C₁中底面边长和侧棱长均为a，侧面A₁ACC₁⊥底面ABC，A₁B=

6

2

a，求异面直线AC与BC₁所成角的余弦值．

科目：gzsx 来源： 题型：

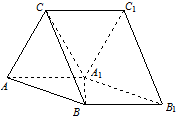
已知三棱柱ABC-A₁B₁C₁，侧面AA₁C₁C⊥侧面ABB₁A₁，AA₁=A₁C=CA=2，AB=A1B=

2

．
（1）求证：AA₁⊥BC；
（2）求二面角A-BC-A₁的余弦值；
（3）若

BD

=2

DB1

，在线段CA₁上是否存在一点E，使得DE∥平
面ABC？若存在，求出CE的长；若不存在，请说明理由．

科目：gzsx 来源： 题型：

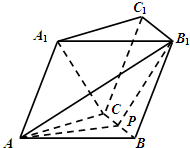
如图，已知三棱柱ABC-A₁B₁C₁的各棱长均为2，P是BC的中点，侧面ACC₁A₁⊥底面ABC，且侧棱AA₁与底面ABC所成的角为60°．
（Ⅰ）证明：直线A₁C∥平面AB₁P；
（Ⅱ）求直线AB₁与平面ACC₁A₁所成角的正弦值．

科目：gzsx 来源： 题型：