精英家教网 >
试题搜索列表 >已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,直线m:y=kx+9,又f′(-1)=0. (1)求函数f(x
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,直线m:y=kx+9,又f′(-1)=0. (1)求函数f(x答案解析
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+bx
2+cx+d满足f(0)=f(x
1)=f(x
2)=0,且0<x
1<x
2.若f(x)在(x
2,+∞)上是增函数,则b的取值范围是
b<0
b<0
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+3x
2-6ax+b在x=2处取得极值9,则a+2b=
.
查看答案和解析>>
科目:gzsx
来源:
题型:
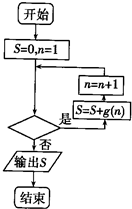
已知函数f(x)=ax
3+
x
2在x=-1处取得极大值,记g(x)=
.程序框图如图所示,若输出的结果S=
,则判断框中可以填入的关于n的判断条件是( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx2-3x(a,b∈R),且f(x)在x=1和x=3处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设函数g(x)=f(x)+t,是否存在实数t,使得曲线y=g(x)与x轴有两个交点,若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx2在x=-1时取得极值,曲线y=f(x)在x=1处的切线的斜率为12;函数g(x)=f(x)+mx,x∈[1,+∞),函数g(x)的导函数g'(x)的最小值为0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求实数m的值;
(Ⅲ) 求证:g(x)≥-7.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+(a-1)x2+48(a-2)x+b的图象关于原点成中心对称.
(1)求a,b的值;
(2)求f(x)的单调区间及极值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx+1的图象经过点(1,-1),且在x=1处f(x)取得极值,
求(1)函数f(x)解析式;
(2)f(x)的单调递增区间.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx+x,若f(2006)=10,则f(-2006)=( )
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•天津一模)已知函数f(x)=ax
3+bx
2在点(2,f(2))处的切线方程为6x+3y-10=0,且对任意的x∈[0,+∞)f'(x)≤kln(x+1)恒成立.
(I)求a,b的值;
(Ⅱ)求实数k的最小值;
(Ⅲ)证明:
| n |
 |
| i=1 |
<ln(n+1)+2(n∈N•).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+bx
2+cx+d(a≠0),图象关于原点对称,且当x=
时,f(x)的极小值为-1,求f(x)的解析式.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+x2+1,x∈(0,1].
(Ⅰ)若f(x)在(0,1]上是增函数,求实数a的取值范围;
(Ⅱ)求f(x)在(0,1]上的最大值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx2+cx在x=±1处取得极值,且在x=0处的切线的斜率为-3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若过点A(2,m)可作曲线y=f(x)的三条切线,求实数m的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+bx
2+(b-a)x(a,b不同时为零的常数),导函数为f′(x).
(1)当
a=时,若存在x∈[-3,-1]使得f′(x)>0成立,求b的取值范围;
(2)求证:函数y=f′(x)在(-1,0)内至少有一个零点;
(3)若函数f(x)为奇函数,且在x=1处的切线垂直于直线x+2y-3=0,关于x的方程
f(x)=-t在[-1,t](t>-1)上有且只有一个实数根,求实数t的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bx2+cx(a≠0)是定义在R上的奇函数,且x=-1时,函数取极值1.
(1)求a,b,c的值;
(2)若x1,x2∈[-1,1],求证:|f(x1)-f(x2)|≤2;
(3)求证:曲线y=f(x)上不存在两个不同的点A,B,使过A,B两点的切线都垂直于直线AB.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2013•延庆县一模)已知函数f(x)=ax3+bx2-2(a≠0)有且仅有两个不同的零点x1,x2,则( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3-3x2+(c+3)x+c+8 在x=-2 时有极值1
(1)极值1是极大值还是极小值,说明理由,并求出f(x) 的另一个极值;
(2)过点A(0,10)作函数f (x)图象的切线l,求直线l与函数g(x)=f(x)+x3-x 的图象围成的平面图形的面积.
查看答案和解析>>
科目:gzsx
来源:
题型:
(2008•和平区三模)已知函数f(x)=ax
3+bx
2+cx+d,(x∈R)在任意一点(x
0,f(x))处的切线的斜率为k=(x
0-2)(x
0+1).
(1)求a,b,c的值;
(2)求函数f(x)的单调区间;
(3)若y=f(x)在-3≤x≤2上的最小值为
,求y=f(x)在R上的极大值.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax3+bsinx+4(a,b∈R),f(lg(log23))=2,则f(lg( log32))=( )
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+bx
2lnx,若f(x)在点(1,f(1))处的切线方程为y=2x-2.
(1)求f(x)的解析式;
(2)求f(x)在[
,e]上的单调区间和最值;
(3)若存在实数m∈[-2,2],函数g(x)=
x3lnx-x
3-(2m+n)x在(1,e)上为单调减函数,求实数n的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax
3+bx
2(x∈R)图象过点P(-1,2),且在点P处的切线恰好与x-3y=0垂直.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数
g(x)=mx3+f′(x)-3x在(2,+∞)上是减函数,求实数m的取值范围.
查看答案和解析>>

 已知函数f(x)=ax3+
已知函数f(x)=ax3+