如图，AD是△ABC的角平分线，如图，AD是△ABC的角平分线，答案解析

科目：czsx 来源：2011年广东省佛山市高中阶段学校招生考试数学试卷 题型：068

如图，一张纸上有线段AB；

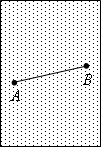
(1)请用尺规作图，作出线段AB的垂直平分线(保留作图痕迹，不写作法和证明)；

(2)若不用尺规作图，你还有其它作法吗？请说明作法(不作图)；

科目：czsx 来源： 题型：阅读理解

（2013•乐山）阅读下列材料：
如图1，在梯形ABCD中，AD∥BC，点M，N分别在边AB，DC上，且MN∥AD，记AD=a，BC=b．若

AM

MB

=

m

n

，则有结论：MN=

bm+an

m+n

．
请根据以上结论，解答下列问题：
如图2，图3，BE，CF是△ABC的两条角平分线，过EF上一点P分别作△ABC三边的垂线段PP₁，PP₂，PP₃，交BC于点P₁，交AB于点P₂，交AC于点P₃．
（1）若点P为线段EF的中点．求证：PP₁=PP₂+PP₃；
（2）若点P为线段EF上的任意位置时，试探究PP₁，PP₂，PP₃的数量关系，并给出证明．

科目：czsx 来源： 题型：

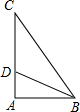
如图所示，∠A=90°，BD是△ABC的角平分线，AC=8cm，DC：AD=3：1，则点D到BC的距离为

2cm

2cm

．

科目：czsx 来源： 题型：

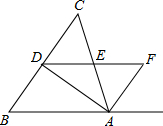
如图，AD是△ABC的角平分线，过点D作直线DF∥BA，交△ABC的外角平分线AF于点F，DF与AC交于点E．
求证：DE=EF．

科目：czsx 来源： 题型：

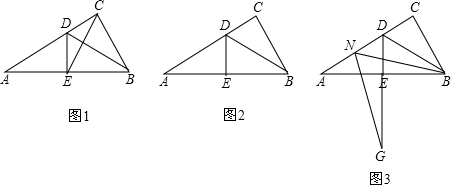
在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB于点E．
（1）如图1，连接EC，求证：△EBC是等边三角形；
（2）点M是线段CD上的一点（不与点C，D重合），以BM为一边，在BM的下方作∠BMG=60°，MG交DE延长线于点G．请你在图2中画出完整图形，并直接写出MD，DG与AD之间的数量关系；
（3）如图3，点N是线段AD上的一点，以BN为一边，在BN的下方作∠BNG=60°，NG交DE延长线于点G．试探究ND，DG与AD数量之间的关系，并说明理由．

科目：czsx 来源： 题型：

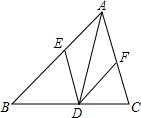
如图△ABC中，DE∥AC交AB于E，DF∥AB交AC于F，
（1）如果AD是△ABC的角平分线，那么四边形AEDF是

菱形

菱形

形．请证明你的结论．
（2）在（1）的条件下，给△ABC再添加一个条件：

∠BAC=90°（答案不唯一）

∠BAC=90°（答案不唯一）

，则四边形AEDF是正方形．（只填空，不要证明）

科目：czsx 来源： 题型：

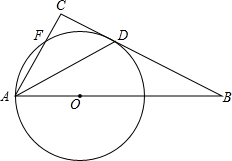
（2013•温州二模）如图，在△ABC中，AD是它的角平分线，∠C=90°，E在AB边上，以AE为直径的⊙O交BC于点D，交AC于点F．
（1）求证：BC是⊙O的切线；
（2）已知∠B=30°，AD的弦心距为1，求AF的长．

科目：czsx 来源： 题型：

6、如图，AD⊥BC，垂足为D，∠BAC=∠CAD，下列说法正确的是（　　）

A、直线AD是△ABC的边BC上的高

B、线段BD是△ABD的边AD上的高

C、射线AC是△ABD的角平分线

D、△ABC与△ACD的面积相等

科目：czsx 来源： 题型：

如图，在△ABC中，AD是高，BE是角平分线，AD、BE交于点F，∠C=30°，∠BFD=70°，求∠BAC的度数．

科目：czsx 来源： 题型：

如图，在△ABC中，∠ACB=90°，AD是△ABC的角平分线，BC=10cm，BD：DC=3：2，则点D到AB的距离为

4cm

4cm

．

科目：czsx 来源： 题型：

如图，AD是△ABC的角平分线，AD的垂直平分线交BC的延长线于点F．
求证：∠FAC=∠B．

科目：czsx 来源： 题型：

在△ABC中，AD是△ABC的角平分线．
（1）如图1，过C作CE∥AD交BA延长线于点E，若F为CE的中点，连接AF，求证：AF⊥AD；
（2）如图2，M为BC的中点，过M作MN∥AD交AC于点N，若AB=4，AC=7，求NC的长．

科目：czsx 来源： 题型：

（2002•上海模拟）如图，在△ABC中，AD是∠BAC的角平分线，AB=3，AC=2，∠BAC=120°，求

AD

AB

的值．

科目：czsx 来源： 题型：

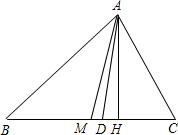
如图，AD、AM、AH分别△ABC的角平分线、中线和高．
（1）因为AD是△ABC的角平分线，所以∠

 

=∠

 

=

1

2

∠

 

；
（2）因为AM是△ABC的中线，所以

 

=

 

=

1

2

 

；
（3）因为AH是△ABC的高，所以∠

 

=∠

 

=90°．

科目：czsx 来源： 题型：

如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，
（1）若∠B=47°，∠C=73°，求∠DAE的度数．
（2）若∠B=α°，∠C=β° （α＜β），求∠DAE的度数（用含α、β的代数式表示）

科目：czsx 来源： 题型：

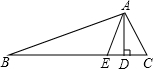
如图，已知△ABC中，AD是高，AE是角平分线．
（1）若∠B=20°，∠C=60°，则∠EAD=

20

20

°；
（2）若∠B=a°，∠C=b°（b＞a），试通过计算，用a、b的代数式表示∠EAD的度数；
（3）特别地，当△ABC为等腰三角形（即∠B=∠C）时，请用一句话概括此时AD和AE的位置关系：

重合

重合

．

科目：czsx 来源： 题型：

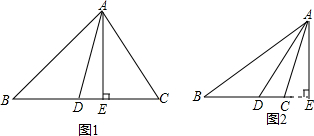
在△ABC中，AD是角平分线，AE是高线
①如图1所示，∠ABC=40°，∠ACB=70°，求∠DAE．
②如图2所示，∠ABC=30°，∠ACB=110°，求∠DAE．
③根据①、②两题的计算结果，请猜想∠DAE与∠ABC和∠ACB之间的关系．（用等式表示出来）

科目：czsx 来源： 题型：

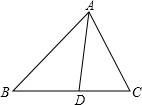
如图，AD是△ABC的角平分线，若AB=10，AC=8，则S_△ABD：S_△ADC=（　　）

A．1：1

B．4：5

C．5：4

D．16：25

科目：czsx 来源： 题型：

如图（1）所示，OP是∠MON的平分线，

（1）请你利用图（1）画出公共边在角平分线OP上的两个全等三角形并将添加的全等条件标注在图上． 
（2）如图（2），在△ABC中，∠ACB=90°，∠B=60°，AD、CE分别是∠BAC，∠BCA的平分线交于F，试判断FE与FD之间的数量关系．
（3）如图（3），在△ABC中，若∠ACB≠90°，而（1）中其他条件不变，请问（1）中所得的结论是否仍然成立？若成立，请证明；若不成立，说明理由．

科目：czsx 来源： 题型：

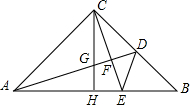
如图，等腰直角三角形△ABC中，∠ACB=90°，点D是BC的中点，CE⊥AD于点F交AB于点E，CH是AB上的高交AD于点G．
（1）找出图中的全等三角形；
（2）找出与∠ADC相等的角，并请说明理由．