若a的2m+n次方b除以a的2次方b的2次方乘以a的n次方b等于a的答案解析

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

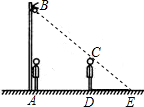
如图，一人从路灯下向前走了6m，发现自己在地面上的影子是2M，若人的身高为1.5m，那么路灯离地面的高度是

 

m．

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

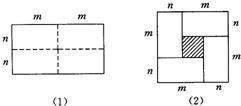
51、（1）图（1）是一个长为2m，宽为2n的矩形，把此矩形沿图中虚线用剪刀均分为四个小长方形，然后按图（2）的形状拼成一个正方形，请问：这两个图形的什么量不变所得的正方形的面积比原矩形的面积多出的阴影部分的面积用含m，n的代数式可表示为

（m-n）²=m²-2mn+n²

；
（2）由（1）的探索可得出的结论是：在周长一定的矩形中，

长和宽相等

时，面积最大；
（3）若矩形的周长为24cm，则当边长为多少时，该图形的面积最大？最大面积是多少？

科目：czsx 来源： 题型：

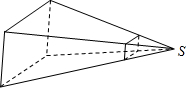
如图，电影胶片上每一个图片的规格为3.5cm×3.5cm，放映屏幕的规格为2m×2m，若放映机的光源S距胶片20cm，那么光源S距屏幕

80

7

80

7

米时，放映的图象刚好布满整个屏幕．

科目：czsx 来源： 题型：

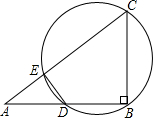
（在下面的（I）（II）两题中选做一题，若两题都做，按第（I）题评分）
（I）如图，在△ABC中，AB=4，BC=3，∠B=90°，点D在AB上运动，但与A、B不重合，过B、C、D三点的圆交AC于E，连接DE．
（1）设AD=x，CE=y，求y与x之间的函数关系式，并指出自变量x的取值范围；
（2）当AD长为关于x的方程2x²+（4m+1）x+2m=0的一个整数根时，求m的值．

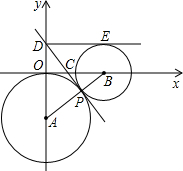
（II）如图，在直角坐标系xOy中，以点A（0，-3）为圆心作圆与x轴相切，⊙B与⊙A外切干点P，B点在x轴正半轴上，过P点作两圆的公切线DP交y轴于D，交x轴于C，
（1）设⊙A的半径为r₁，⊙B的半径为r₂，且r₂=

2

3

r₁，求公切线DP的长及直线DP的函数解析式，
（2）若⊙A的位置、大小不变，点B在X轴正半轴上移动，⊙B与⊙A始终外切．过D作⊙B的切线DE，E为切点．当DE=4时，B点在什么位置？从解答中能发现什么？

科目：czsx 来源： 题型：

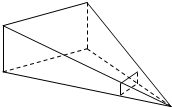
如图，电影胶片上每一个图片的规格为3.5cm×3.5cm，放映屏幕的规格为2m×2m，若放映机的光源S距胶片20cm，要使放映的图象刚好布满整个屏幕，则光源S距屏幕的距离为（　　）

A、 40 7 m

B、 80 7 m

C、 60 7 m

D、15m

科目：czsx 来源： 题型：

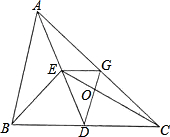
如图，AD为△ABC的中线，BE为△ABD的中线．
（1）在△BED中作BD边上的高，垂足为F；
（2）若△ABC的面积为20，BD=5．
①△ABD的面积为

 

，
②求△BDE中BD边上的高EF的长；
（3）过点E作EG∥BC，交AC于点G，连接EC、DG且相交于点O，若S_△ABC=2m，又S_△COD=n，求S_△GOC．（用含m、n的代数式表示）

科目：czsx 来源： 题型：

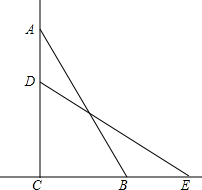
一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直离为8m．若梯子的顶端下滑2m后，低端将水平滑动（　　）m．

A．9米

B．2米

C．3米

D．4米

科目：czsx 来源： 题型：

如图，圆桌正上方的灯泡O（看成一个点）发出的光线照射到桌面后，在地面上形成阴影．若桌面的半径AC=0.8m，桌面与底面的距离AB=1m，灯泡与桌面的距离OA=2m，则地面上阴影部分的面积为

1.44π

1.44π

 m²．（结果保留π）

科目：czsx 来源： 题型：