如图,AD平行BC,AB垂直BC于B,角DCB等于75度,等边三角形答案解析
科目:czsx
来源:素质教育新学案·初中几何·第三册
题型:022
如图所示,直线AB切⊙O于C,∠BCE=75°,∠E=35°,则∠
DCE=________.
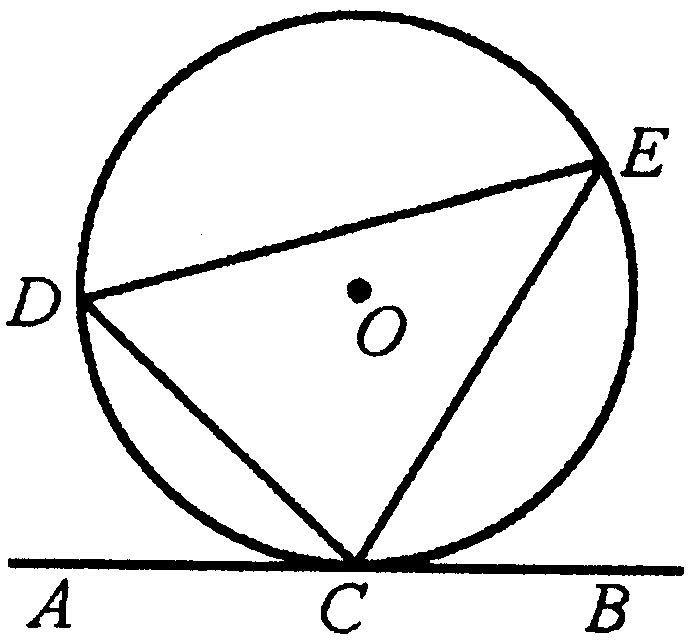
查看答案和解析>>
科目:czsx
来源:
题型:
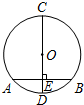
如图,⊙O中弦AB垂直于直径CD于点E,则下列结论:①AE=BE;②
=;③
=;④EO=ED,其中正确的有( )
查看答案和解析>>
科目:czsx
来源:
题型:

25、如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
(1)求证:AB=CD;
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来(不需要证明).
查看答案和解析>>
科目:czsx
来源:
题型:
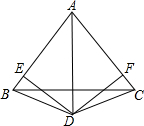
已知,如图,AD是BC的垂直平分线,DE⊥AB于点E,DF⊥AC于点F,
求证:(1)∠ABD=∠ACD;
(2)DE=DF.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
(1)求证:AB=CD;
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来(不需要证明).
查看答案和解析>>
科目:czsx
来源:
题型:
如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
(1)求证:AB=CD
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来(不需要证明).

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
(1)求证:AB=CD;
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来(不需要证明).
查看答案和解析>>
科目:czsx
来源:伴你学数学课 九年级上
题型:044
如图,AD∥EF∥BC,AB∥GH∥CD,EF与GH相交于点O,图中共有多少个平行四边形?
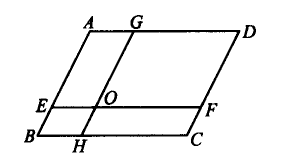
查看答案和解析>>
科目:czsx
来源:同步题
题型:解答题
如图,AD、BC垂直相交于点O,AB∥CD,又BC=8,AD=6,求:AB+CD的长。
查看答案和解析>>
科目:czsx
来源:
题型:

已知:如图,AD、BC相交于点O,AB=CD,AD=CB.
求证:∠A=∠C.
查看答案和解析>>
科目:czsx
来源:
题型:
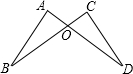
(2013•思明区一模)如图,AD与BC相交于点O,∠A=∠C,添加一个条件
AB=CD(答案不唯一)
AB=CD(答案不唯一)
,使得△ABO≌△CDO.(只需写出一个答案)
查看答案和解析>>
科目:czsx
来源:
题型:
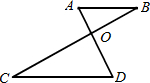
12、如图,AD与BC相交于点O,AB∥CD,若∠B=30°,∠D=60°.则∠BOD=
90
度.
查看答案和解析>>
科目:czsx
来源:
题型:
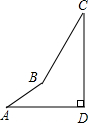
如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°,求AD、CD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
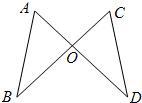
29、如图,AD、BC交于点O,AB=CD,AD=BC,∠A与∠C相等吗?若相等,请给出证明,若不相等,则说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
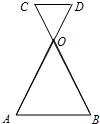
23、如图,AD和BC交于点O,AB∥DC,OA=OB,试说明△OCD是等腰三角形.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是
上一点(点P不与A、C两点重合),连接PC、PD
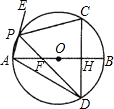
、PA、AD,点E在AP的延长线上,PD与AB交于点F,给出下列四个结论:
(1)CH
2=AH•BH;
(2)
=
;
(3)AD
2=DF•DP;
(4)∠EPC=∠APD,其中正确的个数是( )
查看答案和解析>>
科目:czsx
来源:
题型:

19、如图,AD、BC交于O点,且∠A=∠B,∠C=∠D.求证:AB∥CD.
查看答案和解析>>
科目:czsx
来源:
题型:
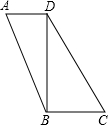
如图,AD=7,AB=25,BC=10,DC=26,DB=24.求:四边形ABCD的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
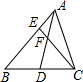
如图,AD是BC边上的中线,F是AD上一点,CF的延长线交AB于点E,若
=,则
=
;若
=,则
=
.
查看答案和解析>>
科目:czsx
来源:
题型:
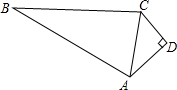
如图,AD⊥CD,AB=13,BC=12,CD=3,AD=4,则sinB=
.
查看答案和解析>>

 如图,⊙O中弦AB垂直于直径CD于点E,则下列结论:①AE=BE;②
如图,⊙O中弦AB垂直于直径CD于点E,则下列结论:①AE=BE;②



 25、如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
25、如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF. 如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.
如图,AD、BC交于点O,EF过点O分别交AB、CD于点E、F.OA=OD,OE=OF.

 (2013•思明区一模)如图,AD与BC相交于点O,∠A=∠C,添加一个条件
(2013•思明区一模)如图,AD与BC相交于点O,∠A=∠C,添加一个条件
 、PA、AD,点E在AP的延长线上,PD与AB交于点F,给出下列四个结论:
、PA、AD,点E在AP的延长线上,PD与AB交于点F,给出下列四个结论:
