练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知函数f(x)=x3+ax2+bx+c

    已知函数f(x)=x3+ax2+bx+c答案解析

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c在x=-
    13
    与x=1    时都取得极值
    （1）求a，b的值及f（x）的单调区间
    （2）若对x∈[-1，2]，f（x）＜c2恒成立，求c的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c，x∈[-2，2]表示的曲线过原点，且在x＝±1处的切线斜率均为-1，有以下命题：

    ①f（x）的解析式为f(x)=x3-4x，x∈[-2，2]；②f（x）的极值点有且仅有一个；③f（x）的最大值与最小值之和等于零.

    其中正确的命题个数为

    A.0                   B.1                    C.2                  D.3

    查看答案和解析>>

    科目：gzsx 来源：2013届河南省高二下第二次月考理科数学试卷（解析版） 题型：解答题

    已知函数f(x)=x3+ax2+bx+c在x=与x=1时都取得极值.

    (1)求a、b的值与函数f(x)的单调区间;

    (2)若对,不等式f(x)<c2恒成立,求c的取值范围.

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：

      已知函数f(x)=x3+ax2+bx+c,曲线y=f(x）在点x=1处的切线为l:3x-y+1=0，若x=时，y=f(x）有极值.

    （1）求a,b,c的值；

    （2）求y=f(x）在［-3，1］上的最大值和最小值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （本题满分12分）已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在x=1处的切线不过第四象限且斜率为3，又坐标原点到切线的距离为，若x=时，y=f(x)有极值.

    （1）求a、b、c的值；w.w.w.k.s.5.u.c.o.m    

    （2）求y=f(x)在[－3,1]上的最大值和最小值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （08年西工大附中文）已知函数f(x)=x3+ax2+bx+c在x=-与x=1时都取得极值．

      (1)求a、b的值及函数f(x)的单调区间；

      (2)若对x∈[－1，2]，不等式f(x)＜c2恒成立，求c的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c，x∈[-2，2]表示的曲线过原点，且在x＝±1处的切线斜率均为-1，有以下命题：

    ①f（x）的解析式为f(x)=x3-4x，x∈[-2，2]；②f（x）的极值点有且仅有一个；③f（x）的最大值与最小值之和等于零.

    其中正确的命题个数为

    A.0                                                 B.1

    C.2                                                 D.3

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c，过曲线y=f(x)上的点P(1，f(1))的切线方程为y=3x+1．

           (Ⅰ)若函数f(x)在x=－2处有极值，求f(x)的表达式；

           (Ⅱ)若函数y=f(x)在区间[－2,1]上单调递增，求实数b的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    17.

        已知函数f(x)=x3+ax2+bx+c在x=-与x=1时都取得极值.

        (1)求a、b的值及函数f(x)的单调区间；

        (2)若对x∈［-1，2］，不等式f(x)＜c2恒成立，求c的取值范围.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c．

    (Ⅰ)若函数f(x)在x=1时有极值且在函数图像上的点(0，1)处的切线与直线3x+y=0平行，求f(x)的解析式；

    (Ⅱ)当f(x)在x∈(0，1)取得极大值且在x∈(1，2)取得极小值时，设点M(b-2，a+1)所在平面区域为S，经过原点的直线L将S分为面积比为1：3的两部分，求直线L的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c在x=与x=1时都取得极值.

    (1)求a、b的值与函数f(x)的单调区间;

    (2)若对x∈［-1,2］,不等式f(x)＜c2恒成立,求c的取值范围.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f ( x ) = x3 + ax2 + bx + c 在x =1 处有极值，f ( x )在x = 2处的切线l不过第四象限且倾斜角为，坐标原点到切线l的距离为。

    （Ⅰ）a、b、c的值；

    （Ⅱ）求函数y = f ( x )在区间上的最大值和最小值。

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c在x=2处有极值,其图象在x=1处的切线平行于直线y=-3x-2,试求函数的极大值与极小值之差.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    (理)已知函数f(x)=x2+lnx+(a-4)x在(1,+∞)上是增函数.

    (1)求实数a的取值范围;

    (2)在(1)的结论下,设g(x)=|ex-a|+,x∈［0,ln3］,求函数g(x)的最小值.

    (文)已知函数f(x)=x3+ax2+bx+c,g(x)=12x-4,若f(-1)=0,且f(x)的图象在点(1,f(1))处的切线方程为y=g(x).

    (1)求实数a、b、c的值;

    (2)求函数h(x)=f(x)-g(x)的单调区间.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x) = x3 + ax2 + bx + c，当x = -1时，f (x)的极大值为7；当x = 3时，f(x)有极小值. 求：

    （1）a、b、c的值；

    （2）函数f(x)的极小值.

    查看答案和解析>>

    科目：gzsx 来源：同步题 题型：解答题

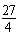    已知函数f(x)=x3+ax2+bx+c的图象如下图，直线y=0在原点处与函数图象相切，且此切线与函数图象所围成的区域(阴影)面积为，求f(x)．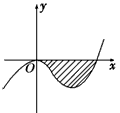

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c在x=1处有极值,f(x)在x=2处的切线l不过第四象限且倾斜角为,坐标原点到切线l的距离为.

    (1)求a、b、c的值;

    (2)求函数y=f(x)在区间［-1,］上的最大值和最小值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c图像上一点M(1,m)处的切线方程为y-2=0，其中a、b、c为常数.

    （1）函数f(x)是否存在单调递减区间？若存在，则求出单调递减区间（用a表示）.

    （2）若x=1不是函数f(x)的极值点，求证：函数f(x)的图像关于点M对称.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线l:3x-y+1=0,若x=,y=f(x)有极值,

    (1)求a,b,c的值;

    (2)求y=f(x)在［-3,1］上的最大值和最小值.

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=x3+ax2+bx+c在x=与x=1时都取得极值.

    (1)求a、b的值与函数f(x)的单调区间;

    (2)若对x∈［-1,2］,不等式f(x)<c2恒成立,求c的取值范围.

    查看答案和解析>>