练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >材料一 《阿房宫赋》：“秦王毕，四海一。”李白

    材料一 《阿房宫赋》：“秦王毕，四海一。”李白答案解析

    科目：gzsx 来源： 题型：阅读理解

    阅读下列材料：

    材料一

    （注：2006年5月第2版第3次印刷的岳麓版必修三第2页图）

    材料二  社会主义道德建设是发展先进文化的重要内容。在新世纪，全面建设小康社会，加快改革开放和现代化建设步伐，顺利实现第三步战略目标，必须在加强社会主义法制建设、依法治国的同时，切实加强社会主义道德建设、以德治国，把法制建设与道德建设、依法治国与以德治国紧密结合起来，通过公民道德建设的不断深化和拓展，逐步形成与发展社会主义市场经济相适应的社会主义道德体系。

                                              ——《公民道德建设实施纲要》

     请回答:

    （1）图中的历史人物是谁？其核心主张是什么？

    （2）早在春秋时期的儒家就提出了“以德治国”的主张，现在党中央也提出了要坚持“以德治国”。那么，我们应如何理解两者的区别呢?

    查看答案和解析>>

    科目：gzsx 来源：吉林省延边州2012届高三下学期复习质量检测数学文科试题 题型：013

    函数f(x)的定义域为R，f(1)＝8，对任意x∈R，(x)＞6，设F(x)＝f(x)－6x－2，则F(x)＞0的解集为

    [　　]
    A．

    阿房宫赋

    B．(－1，1)

    C．(－∞，－1)

    D．(－1，＋∞)

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    2009年12月底某房产公司一次性从银行贷款7亿，自筹资金3亿，总共10亿投资开发一个新的楼盘，此时银行贷款的月利息0.5%，存款的月利息0.3%（除税后），该公司计划从2010年1月底开始每月向银行等额归还本金和利息，并计划用24个月还清全部本金和利息，已知这家房产公司开发的这个新楼盘共建12栋高楼，每栋25层，每层4户，第1层每户卖90万，第2层每户卖92万元，自第2层到第13层，以后每升高一层加2万．14层在13层的基础上减2万，以后每升高一层减2万，假设这家房产公司从开始开发到售完所有房屋仅用2年时间；且买地、买建筑材料，人工成本等各项总开支为6120万元．（数据：1.00524≈1.127，1.00512≈1.062，存款不计复利，贷款计复利，且银行月利息始终固定不变）
    （1）在这一楼盘开发过程中，银行共获得了多少利息？（精确到万元）
    （2）这家地产公司开发完这个楼盘，共获得了多少净收入？（净收入=地产纯收入-自有资金存入银行的所得利息，不计复利，精确到万元）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    随着环保理念的深入，用建筑钢材余料创作城市雕塑逐渐流行．下图是其中一个抽象派雕塑的设计图．图中α表示水平地面，线段AB表示的钢管固定在α上；为了美感，需在焊接时保证：线段AC表示的钢管垂直于α，BD⊥AB，且保持BD与AC异面．
    （1）若收集到的余料长度如下：AC=BD=24（单位长度），AB=7，CD=25，按现在手中的材料，求BD与α应成的角；
    （2）设计师想在AB，CD中点M，N处再焊接一根连接管，然后挂一个与AC，BD同时平
    行的平面板装饰物．但他担心此设计不一定能实现．请你替他打消疑虑：无论AB，CD多长，焊接角度怎样，一定存在一个过MN的平面与AC，BD同时平行（即证明向量
    MN
    与
    AC
    ，
    BD
    共面，写出证明过程）；
    （3）如果事先能收集确定的材料只有AC=BD=24，请替设计师打消另一个疑虑：即MN要准备多长不用视AB，CD长度而定，只与θ有关（θ为设计的BD与α所成的角），写出MN与θ的关系式，并帮他算出无论如何设计MN都一定够用的长度．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

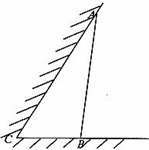    精英家教网如图所示，某饲养场要建造一间两面靠墙的三角形露天养殖场，已知已有两面墙的夹角为60°（即∠C=60°），现有可供建造第三面围墙的材料60米（两面墙的长均大于60米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．
    （1）问当θ为多少时，所建造的三角形露天活动室的面积最大？
    （2）若饲养场建造成扇形，养殖场的面积能比（1）中的最大面积更大？说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某工厂计划出售一种产品，经销人员并不是根据生产成本来确定这种产品的价格，而是通过对经营产品的零售商对于不同的价格情况下他们会进多少货进行调查，通过调查确定了关系式P=-750x+15000，其中P为零售商进货的数量（单位：件），x为零售商支付的每件产品价格（单位：元）．现估计生产这种产品每件的材料和劳动生产费用为4元，并且工厂生产这种产品的总固定成本为7000元（固定成本是除材料和劳动费用以外的其他费用），为获得最大利润，工厂应对零售商每件收取多少元？并求此时的最大利润．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网如图是某一函数的求值流程图，则该函数为
     
    （注：框图中的符号“=”为赋值符号，也可以写成“←”或“：=”）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设变量a、b分别表示一个数，现将a、b交换，用赋值语句描述该算法的结果是：
    c=a，a=b，b=c
    c=a，a=b，b=c
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2003•朝阳区一模）某加油站需要制造一个容积为20πm3的圆柱形储油罐，已知用来制作底面的铁板每平方米价格为40元，用来制作侧面的铁板每平方米价格为32元，若不计制作损耗．
    （Ⅰ）问储油罐底面半径和高各为多少时，制作的储油罐的材料成本价最低？
    （Ⅱ）若制作的储油罐底面铁板半径不能超过1.8m，那么储油罐底面半径的长为多少时，可使制作储油罐的材料成本价最低？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2004•黄埔区一模）要把两种大小不同的钢板截成A、B二种规格的材料，每张钢板可同时截得两种规格较小的钢板数如图表：

    规格类型
    钢板类型    		 A规格 B规格
    第一种钢板 2 1
    第二种钢板 1 2
    今需A、B两种规格材料分别为12及18张．试求：这两种钢板应各取多少张，才能既满足二种规格成品的需要又能使所用钢板总数最少？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=lnx-
    1
    2
    ax2+bx（a＞0），且f′（1）=0
    （1）试用含有a的式子表示b，并求f（x）的单调区间；
    （2）设函数f（x）的最大值为g（a），试证明不等式：g（a）＞ln（1+
    a
    2
    ）-1
    （3）首先阅读材料：对于函数图象上的任意两点A（x1，y1），B（x2，y2）（x1＜x2），如果在函数图象上存在点M（x0，y0）（x0∈（x1，x2）），使得f（x）在点M处的切线l∥AB，则称AB存在“相依切线”特别地，当x0=
    x1+x2
    2
    时，则称AB存在“中值相依切线”．请问在函数f（x）的图象上是否存在两点A（x1，y1），B（x2，y2），使得AB存在“中值相依切线”？若存在，求出一组A、B的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

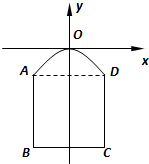    （2012•盐城一模）在综合实践活动中，因制作一个工艺品的需要，某小组设计了如图所示的一个门（该图为轴对称图形），其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成，BC边的长为2t分米（1≤t≤
    3
    2
    ）；曲线AOD拟从以下两种曲线中选择一种：曲线C1是一段余弦曲线（在如图所示的平面直角坐标系中，其解析式为y=cosx-1），此时记门的最高点O到BC边的距离为h1（t）；曲线C2是一段抛物线，其焦点到准线的距离为
    9
    8
    ，此时记门的最高点O到BC边的距离为h2（t）．
    （1）试分别求出函数h1（t）、h2（t）的表达式；
    （2）要使得点O到BC边的距离最大，应选用哪一种曲线？此时，最大值是多少？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    厚度均匀的圆柱形金属饮料罐容积一定时，它的高与底面半径的比为（　　），才能使材料最省？
    A、
    1
    2
    B、2
    C、
    1
    3
    D、3

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    科研人员在某种新型材料的研制中，获得了一组实验数据（如表所示），若准备用下列四个函数中的一个近似地表示这些数据的规律，则其中最接近的一个是（　　）
    x 1.99 3 4 5.1 6.12
    y 1.5 4.04 7.5 12 18.01
    A、y=2x-2
    B、y=
    1
    2
    (x2-1)
    C、y=log2x
    D、y=2x

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    下列四种说法中错误的一项是（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    甲、乙、丙三个同学同时报名参加某重点高校2010年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关才能参加文化测试，文化测试合格者即可获得自主招生入选资格，文化测试合格者即可获得自主招生入选资格，因为甲、乙、丙三人各有优势，甲、乙、丙三人审核过关的概率分别为0.5，0.6，0.4，审核过关后，甲、乙、丙三人文化测试合格的概率分别为0.6，0.5，0.75．
    （1）求甲、乙、丙三人中只有一人通过审核的概率；
    （2）设甲、乙、丙三人中获得自主招生入选资格的人数为ξ，求随机变量ξ的分布列和数学期望

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    精英家教网如图所示，某动物园要为刚入园的小老虎建造一间两面靠墙的三角形露天活动室，已知已有的两面墙的夹角为60°（即∠C=60°且两面墙的长度足够大），现有可供建造第三面围墙的材料6米（即AB长为6米），为了使得小老虎能健康成长，要求所建造的三角形露天活动室尽可能大，记∠ABC=θ．
    （1）当θ=105°时，求所建造的三角形露天活动室的面积．
    （2）问当θ为多少时，所建造的三角形露天活动室的面积最大？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    在某种新型材料的研制中，实验人员获得了下列一组实验数据．现准备用下列四个函数中的一个近似地表示这些数据的规律，其中最接近的一个是（）
    x 1.95 3.00 3.94 5.10 6.12
    y 0.97 1.59 1.98 2.35 2.61

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    某工厂有14m长的旧墙一面，现在准备利用这面旧墙，建造平面图形为矩形，面积为126m2的厂房，工程条件为：①建1m新墙的费用为a元；②修1m旧墙的费用为
    a
    4
    元；③拆去1m旧墙，用所得材料建造1m新墙的费用为
    a
    2
    元．经过讨论有两种方案：
    （Ⅰ）利用旧墙的一段xm（x＜14）为矩形厂房一面的边长；
    （Ⅱ）矩形厂房利用旧墙的一面边长为x（x≥14）．
    问：如何利用旧墙，即x为多少米时，建墙费用最省？（Ⅰ）（Ⅱ）两种方案哪个更好？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知一种材料的最佳加入量在100g到200g之间，若按照0.618法优选，则第2次试点的加入量为
    138.2或161.8
    138.2或161.8
    g．

    查看答案和解析>>