精英家教网 >
试题搜索列表 >在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转
在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转答案解析
科目:czsx
来源:
题型:
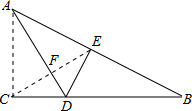
如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=
cm.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC折叠,使点B与点A重合,若S
△ABC=12cm
2,则S
△AEF=
cm
2.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
(1)点B的对应点是
E
E
,AC对应线段是
DC
DC
.
(2)判断△ACD的形状.
(3)求∠BCE的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
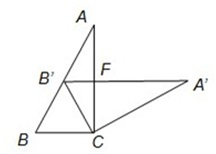
(2009•南平)如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•抚顺一模)在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
(1)如图1,当A′B′∥AC时,设A′C与AB相交于点D.证明:△BCD是等边三角形;
(2)如图2,连接A′A、B′B,设△ACA′和△BCB′的面积分别为S
△ACA′和S
△BCB′.求:S
△ACA′与S
△BCB′的比;
(3)如图3,设AC中点为E,A′B′中点为P,BC=a,连接EP,求:角θ为多少度时,EP长度最大,并求出EP的最大值.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知如图,在平面直角坐标系中,点A(9,0),B(3,0),点C在第一象限,∠ACB=90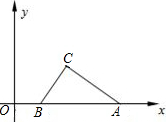 °,∠BAC=30°,将△ABC绕点B逆时针旋转120°.
°,∠BAC=30°,将△ABC绕点B逆时针旋转120°.
(1)直接写出旋转后点A的对应点的坐标;
(2)求旋转过程中线段AC扫过的图形面积.
查看答案和解析>>
科目:czsx
来源:南平
题型:单选题
如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C.
(1)如图1,当A′B′∥AC时,设A′C与AB相交于点D.证明:△BCD是等边三角形;
(2)如图2,连接A′A、B′B,设△ACA′和△BCB′的面积分别为S△ACA′和S△BCB′.求:S△ACA′与S△BCB′的比;
(3)如图3,设AC中点为E,A′B′中点为P,BC=a,连接EP,求:角θ为多少度时,EP长度最大,并求出EP的最大值.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
(1)点B的对应点是______,AC对应线段是______.
(2)判断△ACD的形状.
(3)求∠BCE的度数.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
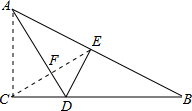 如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=________cm.
如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=________cm.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
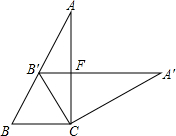 如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)
如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)
- A.
1个
- B.
2个
- C.
3个
- D.
4个
查看答案和解析>>
科目:czsx
来源:福建省期末题
题型:填空题
如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=( )cm。
查看答案和解析>>
科目:czsx
来源:
题型:填空题
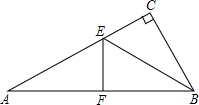 如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC折叠,使点B与点A重合,若S△ABC=12cm2,则S△AEF=________cm2.
如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC折叠,使点B与点A重合,若S△ABC=12cm2,则S△AEF=________cm2.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为( )
查看答案和解析>>
科目:czsx
来源:
题型:
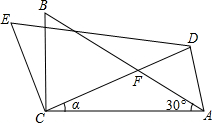
(2011•宁德)如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为
40°或20°
40°或20°
,△ADF是等腰三角形.
查看答案和解析>>
科目:czsx
来源:
题型:单选题
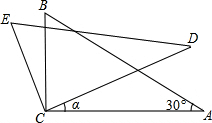 如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为
如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为
- A.
20°
- B.
40°
- C.
20°或40°
- D.
60°
查看答案和解析>>
科目:czsx
来源:福建省中考真题
题型:填空题
如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为( ),△ADF是等腰三角形。
查看答案和解析>>
科目:czsx
来源:
题型:
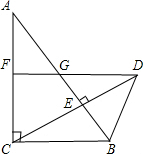
已知,如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.
(1)求证:GE=GF;
(2)若BD=1,求DF的长.
查看答案和解析>>
科目:czsx
来源:
题型:
(2012•南通)如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P
1,此时AP
1=2;将位置①的三角形绕点P
1顺时针旋转到位置②,可得到点P
2,此时AP
2=2+
;将位置②的三角形绕点P
2顺时针旋转到位置③,可得到点P
3,此时AP
3=3+
;…按此规律继续旋转,直到点P
2012为止,则AP
2012等于( )

| | | |
查看答案和解析>>
科目:czsx
来源:
题型:
已知在△ABC中,∠ACB=90°,∠B=30°,AB=2,则AC=
.
查看答案和解析>>

 如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=
如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD= 如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE. (2009•南平)如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )
(2009•南平)如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)( )
 °,∠BAC=30°,将△ABC绕点B逆时针旋转120°.
°,∠BAC=30°,将△ABC绕点B逆时针旋转120°.

 如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°.将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE. 如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=________cm.
如图,在直角三角形纸片ABC中,∠ACB=90°,∠B=30°,将纸片折叠,使AC落在斜边AB上,落点为E,折痕为AD.连接CE交AD于点F,若AF=2cm,则BD=________cm. 如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)
如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图中与△AB'F相似的三角形有(不再添加其它线段)
 如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC折叠,使点B与点A重合,若S△ABC=12cm2,则S△AEF=________cm2.
如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC折叠,使点B与点A重合,若S△ABC=12cm2,则S△AEF=________cm2. 如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为( )
如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为( ) (2011•宁德)如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为
(2011•宁德)如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,当旋转角α度数为 如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为
如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于F,连接AD,△ADF是等腰三角形旋转角α度数为
 已知,如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.
已知,如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB、AC交于点G、F.