练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >2^(n-1)an

    2^(n-1)an答案解析

    科目：gzsx 来源： 题型：

    等差数列{an}中，a2=8，S6=66
    （1）求数列{an}的通项公式an；
    （2）设bn=
    2(n+1)an
    ，Tn=b1+b2+b3+…+bn，求Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设Sn为等差数列{an}的前n项和，a2=8，S5=50
    （I）求数列{an}的通项公式；   
    （II）设bn=
    2(n+1)an
    ，Tn=b1+b2+…+bn    ，求T10．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设x轴、y轴正方向上的单位向量分别是
    i
    、
    j
    ，坐标平面上点An、Bn（n∈N*）分别满足下列两个条件：
    ①
    OA1
    =4
    j
    且
    An-1A
    n    =
    i
    （n∈N*，n≥2）；
    ②
    OB1
    =
    i
    +
    1
    2
    j
    且
    Bn-1Bn
    =-
    1
    n(n+1)
    j
    (n∈N*，n≥2)    ．（其中O为坐标原点）
    （I）求向量
    OAn
    及向量
    OBn
    的坐标；
    （II）设an=
    OAn
    •
    OBn
    ，求an的通项公式并求an的最小值；
    （III）对于（Ⅱ）中的an，设数列bn=
    sin
    nπ
    2
    cos
    (n-1)π
    2
    (n+1)an-6n+3
    ，Sn为bn的前n项和，证明：对所有n∈N*都有Sn＜
    89
    48
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    等差数列{an}中，a2=4，S6=42．
    （1）求数列的通项公式an；
    （2）设bn=
    2(n+1)an
    ，Tn=b1+b2+…+bn，求T6．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知数列{an}的前n项和为Sn，且满足Sn=n2+n(n∈N*)．
    （I）求数列{an}的通项公式；
    （Ⅱ）若bn=
    2(n+1)an
    ，求数列{bn}的前n项和Tn；
    （Ⅲ）若∃n∈N*，使Tn＜C成立，求实数C的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    已知数列{an}的前n项和为Sn，且满足Sn=n2+n(n∈N*)．
    （I）求数列{an}的通项公式；
    （Ⅱ）若bn=
    2
    (n+1)an
    ，求数列{bn}的前n项和Tn；
    （Ⅲ）若∃n∈N*，使Tn＜C成立，求实数C的取值范围．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    等差数列{an}中，a2=4，S6=42．
    （1）求数列的通项公式an；
    （2）设bn=
    2
    (n+1)an
    ，Tn=b1+b2+…+bn，求T6．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    等差数列{an}中，a2=8，S6=66
    （1）求数列{an}的通项公式an；
    （2）设bn=
    2
    (n+1)an
    ，Tn=b1+b2+b3+…+bn，求Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （选做2）已知当a≠b及n∈N*时有公式：an+an-1b+…+arbn-r+…+abn-1+bn=
    bn+1-an+1
    b-a

    （1）利用上述公式证明：对于0＜a＜b，有（n+1）（b-a ） an＜b n+1-an+1＜（n+1）（b-a） bn．
    （2）证明：对一切n∈N*，有（1+
    1
    n
    ）n＜（1+
    1
    n+1
    ）n+1．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

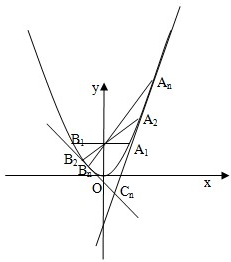    精英家教网如图，对每个正整数n，An（xn，yn）是抛物线x2=4y上的点，过焦点F的直线FAn交抛物线于另一点Bn（sn，tn）．
    （Ⅰ）试证：xnsn=-4（n≥1）；
    （Ⅱ）取xn=2n，并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点．试证：|FC1|+|FC2|+…+|FCn|=2n-2-n+1+1．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知数列{an}中，an=1+
    1a+2(n-1)
    (n∈N*，a∈R，且a≠0)    ．
    （1）若a=-7，求数列{an}中的最大项和最小项的值；
    （2）若对任意的n∈N*，都有an≤a6成立，求a的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知等比数列{an}的首项、公比、前三项的平均值都等于常数a．
    （I）求数列{an}的通项公式；
    （II）设a≠1，n≥2，记bn=
    an
    a2n+an-2
    ，Tn=b2+b3+…+bn    ．
    （i）证明：bn=-
    1
    3
    [
    1
    (-2)n-1-1
    -
    1
    (-2)n-1
    ]    ；
    （ii）若Tn＞
    7
    60
    ，求n的所有可能取值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    数列{an}中，a1=8，a4=2且满足an+2=2an+1-an（ n∈N*）
    （1）求数列{an}的通项公式；
    （2）设Sn=|a1|+|a2|+…+|an|，求Sn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2012•荆州模拟）已知数列{an}中，a1=21，a5=9，满足an+2-2an+1+an=0（n∈N*）
    （1）求数列{an}的通项公式
    （2）设sn=|a1|+|a2|+…|an|，求Sn
    （3）若bn=
    1
    n(27-an)
    ，数列{bn}的前n项和为Tn，是否存在最大的整数p，使得对任意（n∈N*）均有Tn＞
    p
    36
    成立？若存在，求出p，若不存在，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    是否存在常数a，b使等式1-n+2-（n-1）+3-（n-2）+…+n-1=an（n+b）（n+2）对于任意的n∈N+总成立？若存在，求出来并证明；若不存在，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=sinx，数列{an}满足an=
    1
    2
    ，an+1=f(
    π
    2
    an).
    （1）求证：当x∈(0，
    π
    2
    )    时，不等式
    2
    π
    x＜f(x)＜x    恒成立；
    （2）设Sn为数列{an}的前n项和，求证：
    n
    2
    ≤Sn≤
    1
    π-2
    [(
    π
    2
    )n-1].    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2013•江西）正项数列{an}满足
    a
    2
    n
    -（2n-1）an-2n=0．
    （1）求数列{an}的通项公式an；
    （2）令bn=
    1
    (n+1)an
    ，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知xn=a0+a1（x+3）2+…+an-1（x+3）n-1+an（x+2）n，（n≥2）．
    （1）求an和an-1；
    （2）将a0记为第一项系数，a1记为第二项系数，…an记为第n项系数，求式子奇数项系数和．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知数列{an}的前n项和Sn=2+(n-1)(
    1
    2
    )n-1(n∈N*)    ，则存在数列{xn}，{yn}，使得：（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    数列{an}中，a1=2，an+1=
    2(n+1)
    n
    an（n∈N*）．
    （Ⅰ）令bn=
    an
    n
    ，求证数列{bn}是等比数列；
    （Ⅱ）求数列{an}的前n项和Sn．

    查看答案和解析>>