
科目:gzsx 来源: 题型:
.(20分) 已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(1)求双曲线C的方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(天津卷理21文22)已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(本小题满分14分)
已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(20分) 已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(1)求双曲线C的方程;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(2)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源:2013届山东省高二12月月考理科数学 题型:解答题
(本小题满分12分). 已知中心在原点的双曲线C的一个焦点是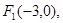 一条渐近线的方程是
一条渐近线的方程是
(1)求双曲线C的方程;
(2)若以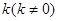 为斜率的直线
为斜率的直线 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求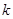 的取值范围.
的取值范围.
科目:gzsx 来源:2008年普通高等学校招生全国统一考试理科数学(天津卷) 题型:解答题
(本小题满分14分)
已知中心在原点的双曲线C的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以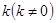 为斜率的直线
为斜率的直线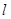 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围.
的取值范围.
科目:gzsx 来源:2013届浙江省高二12月阶段性检测理科数学试卷 题型:解答题
已知中心在原点的双曲线C的一个焦点是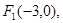 一条渐近线的方程是
一条渐近线的方程是
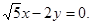
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以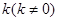 为斜率的直线
为斜率的直线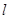 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为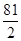 ,求
,求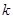 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(天津卷理21文22)已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
(08年天津卷)(本小题满分14分)
已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
已知中心在原点的双曲线C的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是![]() .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,线段MN的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源:广东实验中学2009-2010学年(下)高二级模块考试(理) 题型:解答题
已知中心在原点的双曲线C的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是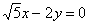 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)若以 为斜率的直线
为斜率的直线 与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为
与双曲线C相交于两个不同的点M,N,且线段MN的垂直平分线与两坐标轴围成的三角形的面积为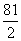 ,求
,求 的取值范围.
的取值范围.
科目:gzsx 来源:2013-2014学年福建省福州市高三上学期期末质量检测理科数学试卷(解析版) 题型:解答题
已知中心在原点的双曲线C的一个焦点是F1(一3,0),一条渐近线的方程是
(1)求双曲线C的方程;
(2)若以k(k≠0)为斜率的直线 与双曲线C相交于两个不同的点M, N,且线段MN的
与双曲线C相交于两个不同的点M, N,且线段MN的
垂直平分线与两坐标轴围成的三角形的面积为 ,求k的取值范围。
,求k的取值范围。
科目:gzsx 来源:2013-2014学年黑龙江省高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知中心在原点的双曲线 的一个焦点是
的一个焦点是 ,一条渐近线的方程是
,一条渐近线的方程是 。
。
(1)求双曲线 的方程;
的方程;
(2)若以 为斜率的直线
为斜率的直线 与双曲线
与双曲线 相交于两个不同的点
相交于两个不同的点 ,且线段
,且线段 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为 ,求
,求 的取值范围。
的取值范围。
科目:gzsx 来源:2010-2011年吉林省高二下学期第一次月考数学试卷 题型:解答题
已知双曲线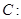
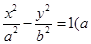 >0,b>0),的一个焦点是
>0,b>0),的一个焦点是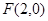 ,离心率
,离心率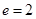 ,
,
(1)求双曲线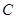 的方程
的方程
(2)若以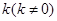 为斜率的直线
为斜率的直线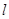 与双曲线
与双曲线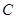 交于两个不同的点
交于两个不同的点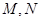 ,线 段
,线 段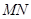 的垂直平分线与两坐标轴围成的三角形的面积为4,求实数
的垂直平分线与两坐标轴围成的三角形的面积为4,求实数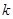 的取值范围.
的取值范围.
科目:gzsx 来源: 题型:
已知中心在原点的双曲线![]() 的一个焦点是
的一个焦点是![]() ,一条渐近线的方程是
,一条渐近线的方程是
![]() .
.
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)若以![]() 为斜率的直线
为斜率的直线![]() 与双曲线
与双曲线![]() 相交于两个不同的点
相交于两个不同的点![]() ,且线段
,且线段![]() 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:gzsx 来源:2010年浙江省宁波市八校联考高二第二学期期末数学(理)试题 题型:解答题
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题 :
(1)若关于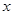 的不等式
的不等式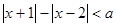 的解集不是空集,求实数
的解集不是空集,求实数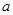 的取值范围;
的取值范围;
(2)已知实数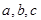 ,满足
,满足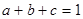 ,求
,求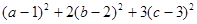 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是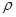 =4cos
=4cos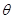 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为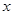 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线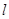 的参数方程是
的参数方程是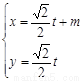 (
(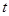 是参数)。
是参数)。
(1)将曲线C的极坐标方程化成直角坐标方程并把直线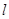 的参数方程转化为普通方程;
的参数方程转化为普通方程;
(2) 若过定点 的直线
的直线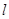 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且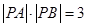 ,试求实数
,试求实数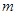 的值。
的值。
科目:gzsx 来源:浙江省宁波市09-10学年高二期末八校联考数学试卷(文科) 题型:解答题
(请考生在下面甲、乙两题中任选一题做答,如果多做,则按所做的甲题计分)
甲题 :
⑴ 若关于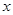 的不等式
的不等式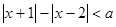 的解集不是空集,求实数
的解集不是空集,求实数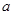 的取值范围;
的取值范围;
⑵
已知实数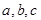 ,满足
,满足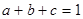 ,求
,求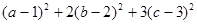 最小值.
最小值.
乙题:
已知曲线C的极坐标方程是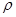 =4cos
=4cos 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为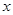 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线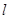 的参数方程是
的参数方程是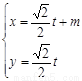 (
( 是参数)。
是参数)。
⑴ 将曲线C的极坐标方程化成直角坐标方程并把直线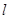 的参数方程转化为普通方程;
的参数方程转化为普通方程;
⑵ 若过定点 的直线
的直线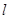 与曲线C相交于A、B两点,且
与曲线C相交于A、B两点,且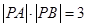 ,试求实数
,试求实数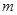 的值。
的值。
科目:gzsx 来源:2013届安徽省蚌埠市高二下学期期中联考文科数学试卷(解析版) 题型:解答题
(本小题满分16分)
已知双曲线C: 的两个焦点为F1(-2,0),F2(2,0),点P
的两个焦点为F1(-2,0),F2(2,0),点P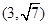 在曲线C上。
在曲线C上。
(1)求双曲线C的方程;
(2)记O为坐标原点,过点Q(0,2)的直线 与双曲线C相交于不同两点E,F,若△OEF的面积为
与双曲线C相交于不同两点E,F,若△OEF的面积为 ,求直线
,求直线 的方程。
的方程。
科目:gzsx 来源: 题型:
(本小题满分14分)
已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点![]() 的直线与椭圆C相交于两点A,B,设P为椭圆上一点,且满足
的直线与椭圆C相交于两点A,B,设P为椭圆上一点,且满足![]() (O为坐标原点),当
(O为坐标原点),当![]() 时,求实数t取值范围.
时,求实数t取值范围.
科目:gzsx 来源:2010年福建省龙岩市高中毕业班第二次质量检查(理) 题型:解答题
已知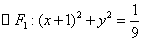 、
、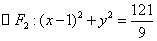 ,椭圆C的方程为
,椭圆C的方程为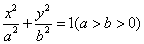 ,
, 、
、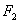 分别为椭圆C的两个焦点,设
分别为椭圆C的两个焦点,设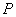 为椭圆C上一点,存在以
为椭圆C上一点,存在以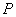 为圆心的
为圆心的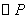 与
与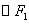 外切、与
外切、与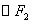 内切
内切
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点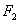 作斜率为
作斜率为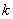 的直线与椭圆C相交于A、B两点,与
的直线与椭圆C相交于A、B两点,与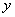 轴相交于点D,若
轴相交于点D,若
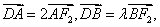 求
求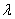 的值;
的值;
(Ⅲ)已知真命题:“如果点T( )在椭圆
)在椭圆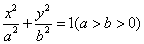 上,那么过点T
上,那么过点T
的椭圆的切线方程为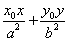 =1.”利用上述结论,解答下面问题:
=1.”利用上述结论,解答下面问题:
已知点Q是直线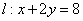 上的动点,过点Q作椭圆C的两条切线QM、QN,
上的动点,过点Q作椭圆C的两条切线QM、QN,
M、N为切点,问直线MN是否过定点?若是,请求出定点坐标;若不是,请说明理由。