科目：czsx 来源：四川省期中题 题型：解答题

已知，如图，ABCD中，AB⊥AC，AB=1，BC=，对角线AC、BD交于O点，将直线AC绕点O顺时针旋转，分别交BC、AD于点E、F。

（1）试说明：当旋转角为90°时，四边形ABEF是平行四边形；
（2）试说明在旋转过程中，线段AF与EC总保持相等；
（3）在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如果能，说明理由并求出此时AC绕O顺时针旋转的度数。

科目：czsx 来源：专项题 题型：证明题

已知，如图，□ABCD中，AB⊥AC，对角线AC、BD交于O点，将直线AC绕点O顺时针旋转，分别交BC、AD于点E、F
（1）证明：当旋转角为90°时，四边形ABEF是平行四边形；
（2）试说明在旋转过程中，线段AF与EC总保持相等。

科目：czsx 来源： 题型：

已知：如图，⊙O中，AB=AC，OD⊥AB于D，OE⊥AC于E．求证：∠ODE=∠OED．

科目：czsx 来源：《第24章 圆》2011年单元测试卷B（西城区）（解析版） 题型：解答题

已知：如图，⊙O中，AB=AC，OD⊥AB于D，OE⊥AC于E．求证：∠ODE=∠OED．

科目：czsx 来源：初三数学圆及旋转题库 第5讲：点和圆的位置关系（解析版） 题型：解答题

已知：如图，⊙O中，AB=AC，OD⊥AB于D，OE⊥AC于E．求证：∠ODE=∠OED．

科目：czsx 来源： 题型：解答题

科目：czsx 来源： 题型：

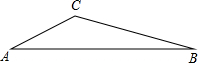
已知：如图在△ABC中，∠A=30°，tanB=

1

3

，BC=

10

，则AB的长为

 

．

科目：czsx 来源： 题型：

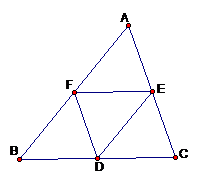
26、已知，如图在△ABC中，点D、E、F分别是BC、CA、AB边上的中点．
求证：（1）四边形AFDE是平行四边形；（2）▱AFDE周长等于AB+AC．

科目：czsx 来源： 题型：

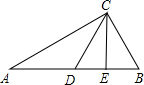
已知，如图在△ABC中，∠ACB=90°，AC=8，BC=6，CD、CE分别是斜边AB上的中线和高．则下列结论错误的是（　　）

A．AB=10

B．CD=5

C．CE= 24 5

D．DE=BE= 5 2

科目：czsx 来源： 题型：

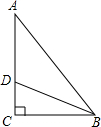
已知：如图在△ABC中，∠C=90°，BD是∠ABC的内角平分线，BC=2

3

，BD=4，求AB和AC．

科目：czsx 来源： 题型：

已知，如图在△ABC中，∠B＞∠C，AD是BC边上的高，AE平分∠BAC．
（1）若∠B=40°，∠C=30°，则∠DAE=

 

；
（2）若∠B=80°，∠C=40°，则∠DAE=

 

；
（3）由（1）、（2）我能猜想出∠DAE与∠B、∠C之间的关系为

 

．理由如下：

科目：czsx 来源： 题型：

已知，如图在△ABC中，AD是BC边上的高线，CE是AB边上的中线，DG平分∠CDE，DC=AE，
求证：CG=EG．
证明：∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=

1

2

AB

1

2

AB

（直角三角形斜边上的中线等于斜边的一半）
又∵AE=

1

2

AB
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是

等腰

等腰

三角形
∵DG平分∠CDE
∴CG=EG（

等腰三角形三线合一

等腰三角形三线合一

）

科目：czsx 来源： 题型：

已知，如图在△ABC中，AB=AC，点D是AC的中点，直线AE∥BC，过D点作直线EF∥AB分别交AE、BC于点E、F，求证：四边形AECF是矩形．

科目：czsx 来源： 题型：

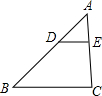
已知：如图在△ABC中，DE∥BC，

AD

DB

=

1

3

，则

DE

BC

=（　　）

A、 1 2

B、 1 3

C、 1 4

D、 1 5

科目：czsx 来源： 题型：

已知：如图在△ABC中，AC=BC，∠ACB=90°，点F在BC的延长线上，点E在AC上，且CF=CE，试判断BE与AF的关系，并证明你的结论．

科目：czsx 来源： 题型：

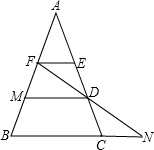
已知：如图在△ABC中，AE=ED=DC，FE∥MD∥BC，FD的延长线交BC的延长线于N，则

EF

BN

为（　　）

A、 1 2

B、 1 3

C、 1 4

D、 1 5

科目：czsx 来源： 题型：

已知，如图在△ABC中，AD为BC边上的高线，AE平分∠BAC，∠C=66°，∠B=34°，则∠EAD的度数是

16°

16°

．

科目：czsx 来源： 题型：

已知：如图在△ABC中，∠C=90°，AD平分∠BAC，交BC于D，若BC=32，且BD：CD=9：7，求：D到AB边的距离．

科目：czsx 来源： 题型：

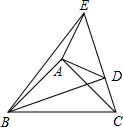
（2013•绥化）已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：
①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE²=2（AD²+AB²），
其中结论正确的个数是（　　）

A．1

B．2

C．3

D．4

科目：czsx 来源： 题型：

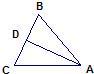
9、已知：如图在△ABC中，AD平分∠BAC，AD⊥BC，则△ACD≌△ABD的根据是

ASA

．