如图1,已知矩形ABCD,点C是边DE的中点,且AB=2AD答案解析
科目:czsx
来源:
题型:
22、如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.

查看答案和解析>>
科目:czsx
来源:2011年山东省济南市初中学业水平模拟考试数学试卷(解析版)
题型:解答题
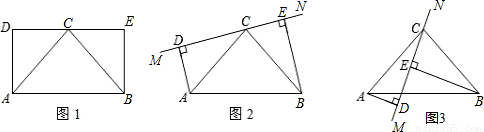
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:山东省中考真题
题型:解答题
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD。
(1)判断△ABC的形状,并说明理由;
(2)保持图1中ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明。
查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《四边形》(08)(解析版)
题型:解答题
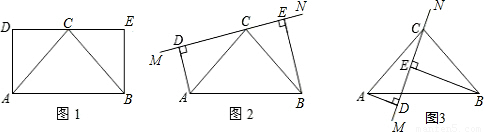
(2010•临沂)如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:2011-2012学年苏科版九年级(上)月考数学试卷(10月份)(解析版)
题型:解答题
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.

查看答案和解析>>
科目:czsx
来源:2010-2011学年安徽省马鞍山市红星中学九年级(上)期中数学试卷(解析版)
题型:解答题
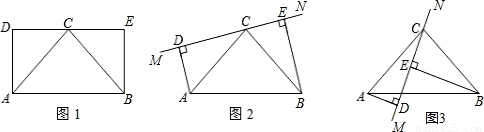
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:2010年全国中考数学试题汇编《三角形》(13)(解析版)
题型:解答题
(2010•临沂)如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.

查看答案和解析>>
科目:czsx
来源:2010年山东省临沂市中考数学试卷(解析版)
题型:解答题
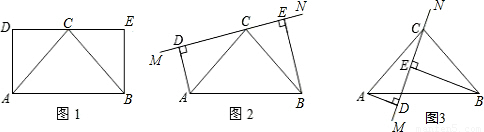
(2010•临沂)如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:2012年辽宁省沈阳市中考数学模拟试卷(四)(解析版)
题型:解答题
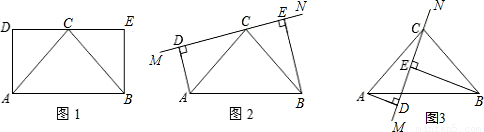
如图1,已知矩形ABED,点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:四边形ABED中,AD⊥DE、BE⊥DE.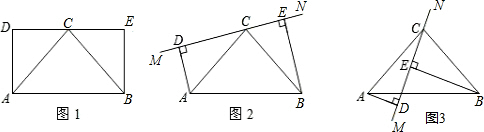
(1)如图1,点C是边DE的中点,且AB=2AD=2BE.判断△ABC的形状:______(不必说明理由);
(2)保持图1中△ABC固定不变,将直线DE绕点C旋转到图2中所在的MN的位置(垂线段AD、BE在直线MN的同侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(垂线段AD、BE在直线MN的异侧).(2)中结论是否依然成立,若成立请证明;若不成立,请写出新的结论,并给予证明.
查看答案和解析>>
科目:czsx
来源:
题型:
如图5,已知矩形ABCD中,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)证明:△AEF≌△DCE;
(2)若DE=4cm,CD=6 cm,求矩形ABCD的周长.

查看答案和解析>>
科目:czsx
来源:
题型:
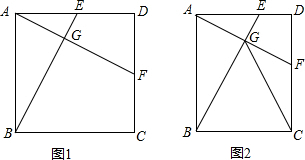
已知矩形ABCD,点E﹑F分别在边AD﹑CD上,且AF⊥BE于点G,AD=mAB,AD=nAE.
(1)如图1,当m=1,n=2时,则
=
1
1
,
=
1
1
;
(2)在(1)的条件下,连接CG,求证:CG=CB;
(3)如图2,对于矩形ABCD,若CG=CB,则m﹑n必满足的数量关系是
n=2m2
n=2m2
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
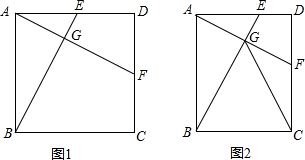
已知矩形ABCD,点E﹑F分别在边AD﹑CD上,且AF⊥BE于点G,AD=mAB,AD=nAE.
(1)如图1,当m=1,n=2时,则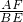 =______,
=______, =______;
=______;
(2)在(1)的条件下,连接CG,求证:CG=CB;
(3)如图2,对于矩形ABCD,若CG=CB,则m﹑n必满足的数量关系是______.
查看答案和解析>>
科目:czsx
来源:
题型:
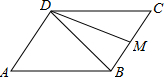
(2012•嘉定区一模)如图,已知平行四边形ABCD,点M是边BC的中点.设
=,
=.用向量
、
表示向量
,
=
.
查看答案和解析>>
科目:czsx
来源:
题型:
已知矩形ABCD中,一边是另一边的2倍且对角线长为3,则矩形的面积为
.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
已知矩形ABCD中,一边是另一边的2倍且对角线长为3,则矩形的面积为________.
查看答案和解析>>
科目:czsx
来源:辽宁省期末题
题型:填空题
已知矩形ABCD中,一边是另一边的2倍且对角线长为3,则矩形的面积为( ).
查看答案和解析>>
科目:czsx
来源:
题型:
5、如图所示,在正方形ABCD中,E是AC上的一点,且AB=AE,则∠EBC的度数是( )

查看答案和解析>>
科目:czsx
来源:
题型:单选题
 如图所示,在正方形ABCD中,E是AC上的一点,且AB=AE,则∠EBC的度数是
如图所示,在正方形ABCD中,E是AC上的一点,且AB=AE,则∠EBC的度数是
- A.
45度
- B.
30度
- C.
22.5度
- D.
20度
查看答案和解析>>














 =______,
=______,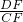 =______;
=______;
 (2012•嘉定区一模)如图,已知平行四边形ABCD,点M是边BC的中点.设
(2012•嘉定区一模)如图,已知平行四边形ABCD,点M是边BC的中点.设