科目:gzsx 来源: 题型:
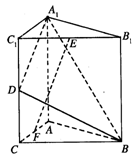
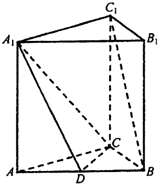 (2011•河北区一模)已知直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=
(2011•河北区一模)已知直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=| 3 |
| 3 |
科目:gzsx 来源:2011年天津市河北区高考数学一模试卷(文科)(解析版) 题型:解答题
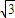 ,
, .
.
科目:gzsx 来源: 题型:
 直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=
直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=| 3 |
| 3 |
科目:gzsx 来源:2008-2009学年北京市海淀区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
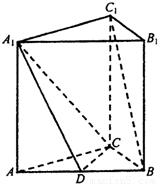 直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,
直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1, ,
, .
.科目:gzsx 来源: 题型:
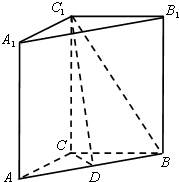 在直三棱柱A1B1C1-ABC中,AC⊥BC,D为AB中点,CB=1,AC=
在直三棱柱A1B1C1-ABC中,AC⊥BC,D为AB中点,CB=1,AC=| 3 |
| 1 |
| 4 |
科目:gzsx 来源: 题型:
 如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC,
如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC,| 6 |
| 3 |
科目:gzsx 来源: 题型:解答题
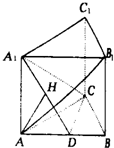 如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC,
如图,已知直三棱柱A1B1C1-ABC中,D为AB的中点,A1D⊥AB1,且AC=BC,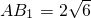 ,
,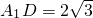 ,求三棱锥A1-ACD的体积;
,求三棱锥A1-ACD的体积;科目:gzsx 来源:2009-2010学年湖北省武汉市华中师大一附中高二(下)期末总复习试卷(立体几何)(解析版) 题型:解答题
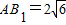 ,
,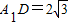 ,求三棱锥A1-ACD的体积;
,求三棱锥A1-ACD的体积;
科目:gzsx 来源: 题型:
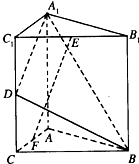 (2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.科目:gzsx 来源: 题型:
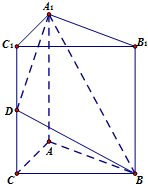 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.科目:gzsx 来源: 题型:
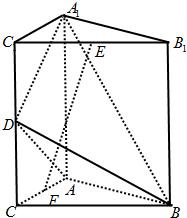 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.科目:gzsx 来源: 题型:
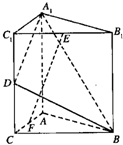 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.科目:gzsx 来源: 题型:
 如图,在直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB,D、E分别是棱C1C、B1C1的中点.
如图,在直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB,D、E分别是棱C1C、B1C1的中点.科目:gzsx 来源: 题型:
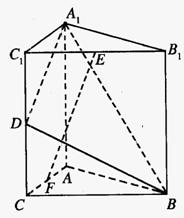
(08年南昌市一模理)(12分)如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(2)求二面角B―A1D―A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由.
科目:gzsx 来源: 题型:
(08年福州质检二文)(12分)
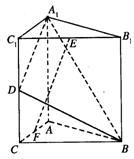
如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)点F是线段AC的中点,证明:EF⊥平面A1BD.
科目:gzsx 来源: 题型:
(08年长郡中学二模理)(12分) 如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
科目:gzsx 来源: 题型:
(本小题满分12分)
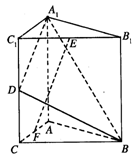
如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB.
D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
科目:gzsx 来源: 题型:
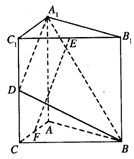
(08年黄冈中学二模)如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
科目:gzsx 来源: 题型:
(08年福州质检二)(12分)
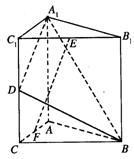
如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.
科目:gzsx 来源: 题型:
(08年长郡中学二模理)(12分) 如图,直三棱柱A1B1C1―ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(Ⅰ)求![]() 与平面A1C1CA所成角的大小;
与平面A1C1CA所成角的大小;
(Ⅱ)求二面角B―A1D―A的大小;
(Ⅲ)试在线段AC上确定一点F,使得EF⊥平面A1BD.