精英家教网 >
试题搜索列表 >如图,点A的坐标是(2,0),点C的坐标是(0,2),点B是直线x=2上一个动点,并且在第一象限,AC、BO交于点D,抛物线y1=ax2+bx+c经过点B、C、D。 (1)求直线AC的函数表达式; (2)如果AB<OC,求抛物线的顶点的横坐标的范围; (3)设经过O、D、A三点的抛物线y2=mx2+nx+p,试判断抛物线y2=mx2+nx+p的顶点与抛物线y1=ax2+bx+c的位置关系,并说明理由。
如图,点A的坐标是(2,0),点C的坐标是(0,2),点B是直线x=2上一个动点,并且在第一象限,AC、BO交于点D,抛物线y1=ax2+bx+c经过点B、C、D。 (1)求直线AC的函数表达式; (2)如果AB<OC,求抛物线的顶点的横坐标的范围; (3)设经过O、D、A三点的抛物线y2=mx2+nx+p,试判断抛物线y2=mx2+nx+p的顶点与抛物线y1=ax2+bx+c的位置关系,并说明理由。答案解析
科目:czsx
来源:
题型:
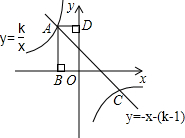
如图,矩形ABOD的顶点A是函数y=
与函数y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.
(1)求两函数的解析式.
(2)求两函数的交点A、C的坐标.
(3)若点P是y轴上一动点,且S
△APC=5,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:Rt△ABC斜边上的高为2.4,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合,直角顶点C落在y轴正半轴上,点A的坐标为(-1.8,0).
(1)求点B的坐标和经过点A、B、C的抛物线的关系式;
(2)如图①,点M为线段AB上的一个动点(不与点A、B重合),MN∥AC,交线段BC于点N,MP∥BC,交线段AC于点P,连接PN,△MNP是否有最大面积?若有,求出△MNP的最大面积;若没有,请说明理由;
(3)如图②,直线l是经过点C且平行于x轴的一条直线,如果△ABC的顶点C在直线l上向右平移m,(2)中的其它条件不变,(2)中的结论还成立吗?请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
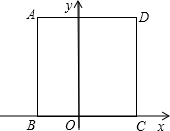
(2012•保定一模)如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点D的坐标是(3,4),则点B的坐标是
(-1,0)
(-1,0)
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,点O是坐标系原点,直线y=kx+b与x轴交于点A,与直线y=-x+5交于点B,点B的纵坐标是3,且AB=5,直线y=-x+5与y轴交于点C.
(1)求直线y=kx+b的解析式;
(2)求△ABC的面积;
(3)在直线BC上是否存在一点P,使△POC的面积是△BOC面积的一半?若不存在,请说明理由;若存在,求出点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
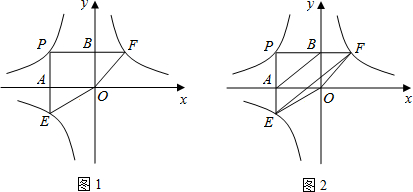
如图,点P是双曲线y=
-(x<0)上一动点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=
于E、F两点.
(1)图1中,四边形PEOF的面积S
1=
18
18
;
(2)图2中,设P点坐标为(-4,3).
①判断EF与AB的位置关系,并证明你的结论;
②记S
2=S
△PEF-S
△OEF,求S
2.
查看答案和解析>>
科目:czsx
来源:
题型:
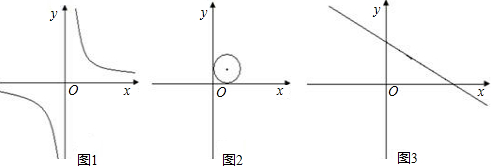
若⊙P与函数图象有且只有一个公共点,并且与x轴、y轴都相切的圆,则称⊙P是这个函数的伴圆.
(1)如图1,求
y=的伴圆的圆心P的坐标及半径r;
(2)如图2,⊙P的半径为1,若⊙P是二次函数y=ax
2+bx+c的伴圆,写出满足要求的开口方向不同的两个二次函数的解析式;
(3)如图3,求一次函数
y=-x+3的所有伴圆的圆心P的坐标及半径.
查看答案和解析>>
科目:czsx
来源:
题型:
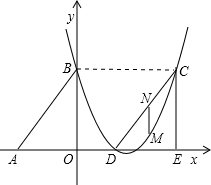
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,点O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线
y=x2-x+c经过B点.
(1)请写出抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,线段CD下方的抛物线上有一个动点M.过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
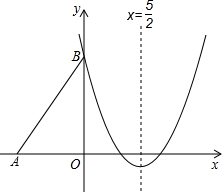
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
x
2+bx+c经过点B,且顶点在直线x=
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
(4)在(2)、(3)的条件下,若点M是线段OB上的一个动点(点M与点O、B不重合),过点M作∥BD交x轴于点N,连接PM、PN,设OM的长为t,△PMN的面积为S,求S和t的函数关系式,并写出自变量t的取值范围,S是否存在最大值?若存在,求出最大值和此时M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,正方形OABC的面积为16,点O为坐标原点,点B在函数y=
(k>0,x>0)的图象上,点P(m,n)是函数y=
(k>0,x>0)的图象上任意一点,过点P分别作x轴、y轴
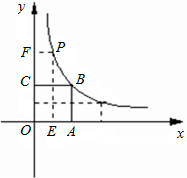
的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
(1)求B点坐标和k的值;
(2)当S=8时,求点P的坐标;
(3)写出S与m的函数关系式.
查看答案和解析>>
科目:czsx
来源:
题型:

某密闭容器内的CO
2(二氧化碳)密度ρ是体积V的反比例函数关系,如图:点A在图象上的一个动点,且S
Rt△ABO=1.
(1)求密度ρ与体积V的函数解析式?
(2)任意写出A点的三个坐标?
查看答案和解析>>
科目:czsx
来源:
题型:
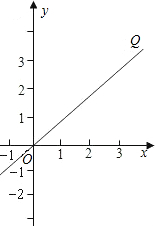
如图,直线OQ的函数解析式为y=x.
下表是直线a的函数关系中自变量x与函数y的部分对应值.
| x |
… |
-1 |
1 |
2 |
3 |
… |
| y |
… |
8 |
4 |
2 |
0 |
… |
设直线a与x轴交点为B,与直线OQ交点为C,动点P(m,0)(0<m<3)在OB上移动,过点P作直线l与x轴垂直.
(1)根据表所提供的信息,请在直线OQ所在的平面直角坐标系中画出直线a的图象,并说明点(10,-10)不在直线a的图象上;
(2)求点C的坐标;
(3)设△OBC中位于直线l左侧部分的面积为S,写出S与m之间的函数关系式;
(4)试问是否存在点P,使过点P且垂直于x轴的直线l平分△OBC的面积?若有,求出点P坐标;若无,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,直线l
1的解析表达式为y=-x+6,且l
1与x轴交于点A,直线l
2的解析表达式为
y=kx-经过点B(1,0)与直线l
1交于点C.
(1)求点A的坐标;
(2)求直线l
2的解析表达式;
(3)求△ABC的面积;
(4)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:在如图1所示的平面直角坐标系xOy中,A、C两点的坐标分别为A(4,2),C(n,-2)(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O-A-B-C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
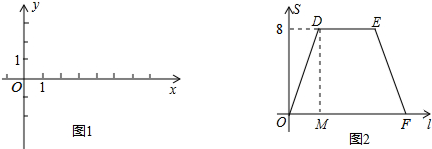
(1)结合以上信息及图2填空:图2中的m=
;
(2)求B、C两点的坐标及图2中OF的长.
查看答案和解析>>
科目:czsx
来源:
题型:
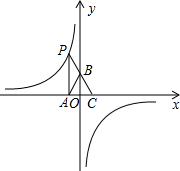
(2013•丽水)如图,点P是反比例函数y=
(k<0)图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
.
(1)k的值是
-4
-4
;
(2)若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是
.
查看答案和解析>>
科目:czsx
来源:
题型:
按要求画图并填空:
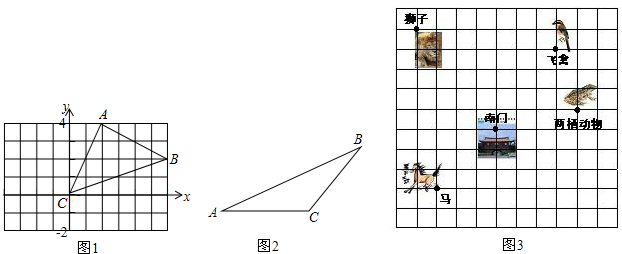
(1)△ABC在如图1所示的平面直角坐标系中,将其平移后得△A′B′C′,若B的对应点B′的坐标是(4,1).
①在图中画出△A′B′C′;
②此次平移可看作将△ABC向
左
左
平移了
2
2
个单位长度,再向
下
下
平移了
1
1
个单位长度得△A′B′C′;
③△A′B′C′的面积为
10
10
.
(2)已知:如图2,△ABC,请在图中作出它的角平分线BD,中线CE和BC边上的高AF.
(3)如图3,这是一个动物园游览示意图,试建立一个适当的平面直角坐标系描述这个动物园图中每个景点位置,(画出图形,并写出各景点的坐标).
查看答案和解析>>
科目:czsx
来源:
题型:

如图,矩形A′BC′O′是矩形ABCO绕点B顺时针旋转得到的.其中点O',C在x轴负半轴上,线段OA在y轴正半轴上,B点的坐标为(-1,3).
(1)如果二次函数y=ax
2+bx+c(a≠0)的图象经过O、O′两点且图象顶点M的纵坐标为
-1.求这个二次函数的解析式;
(2)求边O′A′所在直线的解析式;
(3)在(1)中求出的二次函数图象上是否存在点P,使得
S△PO′M=3S△CO′D,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
阅读材料:
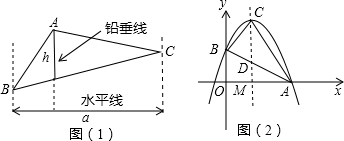
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
如图2,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),点P是抛物线(在第一象限内)上的一个动点.
(1)求抛物线的解析式;
(2)若点B为抛物线与y轴的交点,求直线AB的解析式;
(3)设点P是抛物线(第一象限内)上的一个动点,是否存在一点P,使S
△PAB=S
△CAB?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
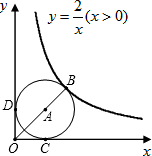
如图,点B是函数
y=(x>0)图象上一点,点A是线段OB上一点,以AB为半径作⊙A恰好与x轴、y轴分别切于点C和点D,则点A的坐标是
.
查看答案和解析>>
科目:czsx
来源:
题型:
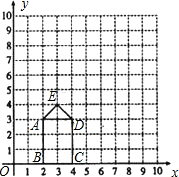
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
(1)求经过A、E、D三点的抛物线的解析式.
(2)以原点为位似中心,将五边形ABCDE放大.
①若放大后的五边形的边长是原五边形对应边长的2倍,请在网格中画出放大后的五边形A
2B
2C
2D
2E
2,并直接写出经过A
2、D
2、E
2三点的抛物线的解析式:
;
②若放大后的五边形的边长是原五边形对应边长的k倍,请你直接写出经过A
k、D
k、E
k三点的抛物线的解析式:
(用含k的字母表示).
查看答案和解析>>
科目:czsx
来源:
题型:
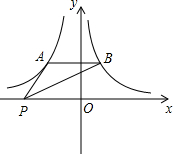
(2013•太原二模)如图,点A是反比例函数y=-
(x<0)图象上的一点,过点A作AB∥x轴,交反比例函数y=
(x>0)的图象于点B,点P是x轴上的一个动点,若△PAB为等腰三角形,则点P的坐标为
(
-3,0);P(-
-3,0),P(
+1,0);P(-
+1,0),P(-1,0)
(
-3,0);P(-
-3,0),P(
+1,0);P(-
+1,0),P(-1,0)
.
查看答案和解析>>

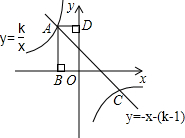 如图,矩形ABOD的顶点A是函数y=
如图,矩形ABOD的顶点A是函数y=
 如图,点O是坐标系原点,直线y=kx+b与x轴交于点A,与直线y=-x+5交于点B,点B的纵坐标是3,且AB=5,直线y=-x+5与y轴交于点C.
如图,点O是坐标系原点,直线y=kx+b与x轴交于点A,与直线y=-x+5交于点B,点B的纵坐标是3,且AB=5,直线y=-x+5与y轴交于点C.

 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,点O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,点O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= (2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
(2012•兰州)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况)
的垂线,垂足分别为E、F,并设矩形OEPF和正方形OABC不重合部分的面积为S.(提示:考虑点P在点B的左侧或右侧两种情况) 某密闭容器内的CO2(二氧化碳)密度ρ是体积V的反比例函数关系,如图:点A在图象上的一个动点,且SRt△ABO=1.
某密闭容器内的CO2(二氧化碳)密度ρ是体积V的反比例函数关系,如图:点A在图象上的一个动点,且SRt△ABO=1.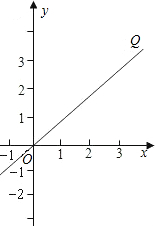 如图,直线OQ的函数解析式为y=x.
如图,直线OQ的函数解析式为y=x. 如图,直线l1的解析表达式为y=-x+6,且l1与x轴交于点A,直线l2的解析表达式为y=kx-
如图,直线l1的解析表达式为y=-x+6,且l1与x轴交于点A,直线l2的解析表达式为y=kx-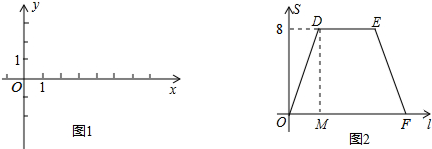
 (2013•丽水)如图,点P是反比例函数y=
(2013•丽水)如图,点P是反比例函数y=
 如图,矩形A′BC′O′是矩形ABCO绕点B顺时针旋转得到的.其中点O',C在x轴负半轴上,线段OA在y轴正半轴上,B点的坐标为(-1,3).
如图,矩形A′BC′O′是矩形ABCO绕点B顺时针旋转得到的.其中点O',C在x轴负半轴上,线段OA在y轴正半轴上,B点的坐标为(-1,3).
 如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED. (2013•太原二模)如图,点A是反比例函数y=-
(2013•太原二模)如图,点A是反比例函数y=-