科目：czsx 来源：江苏省如皋市教育共同体2012届九年级上学期期中考试数学试题 题型：022

科目：czsx 来源：2008年金湖县吕良中学第二次适应性中考模拟试题、数学 题型：022

如图，半圆A和半圆B均与y轴相切于点O，其直径CD，EF均和x轴垂直，以O为顶点的两条抛物线分别经过点C，E和点D，F，则图中阴影部分的面积是________．

科目：czsx 来源： 题型：022

如图，半圆A和半圆B均与y轴相切于点O，其直径CD、EF均和x轴垂直，以O为顶点的两条抛物线分别经过点C、E和点D、F，则图中阴影部分的面积是　　 。

科目：czsx 来源： 题型：022

科目：czsx 来源： 题型：

如图，半圆A和半圆B均与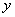轴相切于点O， 其直径CD、EF均和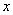轴垂直，以O为顶点的两条抛物线分别经过点C、E和点D、F，则图中阴影部分的面积是      ．

 

科目：czsx 来源： 题型：

如图，在直角坐标系中，⊙M与y轴相切于点C，与x轴交于A（x₁，0），B（x₂，0）两点，其中x₁，x₂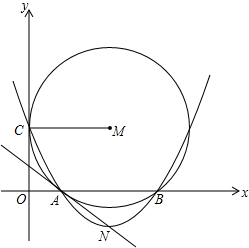是方程x²-10x+16=0的两个根，且x₁＜x₂，连接MC，过A、B、C三点的抛物线的顶点为N．
（1）求过A、B、C三点的抛物线的解析式；
（2）判断直线NA与⊙M的位置关系，并说明理由；
（3）一动点P从点C出发，以每秒1个单位长的速度沿CM向点M运动，同时，一动点Q从点B出发，沿射线BA以每秒4个单位长度的速度运动，当P运动到M点时，两动点同时停止运动，当时间t为何值时，以Q、O、C为顶点的三角形与△PCO相似？

科目：czsx 来源： 题型：

（2013•黄石模拟）如图，在直角坐标系中，⊙P与y轴相切于点C，与x轴交于A（x₁，0），B（x₂，0）两点，其中x₁，x₂是方程x²-10x+16=0的两个根，且x₁＜x₂，连接BC，AC．
（1）求过A、B、C三点的抛物线的解析式；
（2）在抛物线的对称轴上是否存在点Q，使△QAC的周长最小？若存在求出点Q的坐标；若不存在，请说明理由；
（3）点M在第一象限的抛物线上，当△MBC的面积最大时，求点M的坐标．

科目：czsx 来源： 题型：

已知：如图，在直角坐标系中，⊙C与y轴相切于点O，且C点的坐标为（1，0），直线l过点A（-1，0）与⊙C切于D点．D点坐标为

 

，在直线l上存在点P，使△APC为等腰三角形，则P点的坐标

 

．

科目：czsx 来源： 题型：解答题

科目：czsx 来源：2013届湖北省襄阳市襄州区中考适应性考试数学试卷（带解析） 题型：解答题

科目：czsx 来源：2012-2013学年湖北省襄阳市襄州区中考适应性考试数学试卷（解析版） 题型：解答题

科目：czsx 来源：2013年湖北省黄石市中考适应性测试数学试卷（解析版） 题型：解答题

如图，在直角坐标系中，⊙P与y轴相切于点C，与x轴交于A（x₁，0），B（x₂，0）两点，其中x₁，x₂是方程x²-10x+16=0的两个根，且x₁＜x₂，连接BC，AC．
（1）求过A、B、C三点的抛物线的解析式；
（2）在抛物线的对称轴上是否存在点Q，使△QAC的周长最小？若存在求出点Q的坐标；若不存在，请说明理由；
（3）点M在第一象限的抛物线上，当△MBC的面积最大时，求点M的坐标．

科目：czsx 来源：2013年湖北省襄阳市襄州区中考适应性考试数学试卷（解析版） 题型：解答题

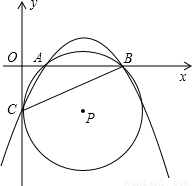
如图，在直角坐标系中，⊙P与y轴相切于点C，与x轴交于A（x₁，0），B（x₂，0）两点，其中x₁，x₂是方程x²-10x+16=0的两个根，且x₁＜x₂，连接BC，AC．
（1）求过A、B、C三点的抛物线的解析式；
（2）在抛物线的对称轴上是否存在点Q，使△QAC的周长最小？若存在求出点Q的坐标；若不存在，请说明理由；
（3）点M在第一象限的抛物线上，当△MBC的面积最大时，求点M的坐标．

科目：czsx 来源：2012年湖北省襄阳市枣阳市普通高中推荐招生考试数学模拟试卷（解析版） 题型：解答题

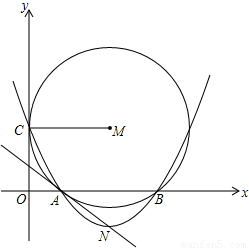
如图，在直角坐标系中，⊙M与y轴相切于点C，与x轴交于A（x₁，0），B（x₂，0）两点，其中x₁，x₂是方程x²-10x+16=0的两个根，且x₁＜x₂，连接MC，过A、B、C三点的抛物线的顶点为N．
（1）求过A、B、C三点的抛物线的解析式；
（2）判断直线NA与⊙M的位置关系，并说明理由；
（3）一动点P从点C出发，以每秒1个单位长的速度沿CM向点M运动，同时，一动点Q从点B出发，沿射线BA以每秒4个单位长度的速度运动，当P运动到M点时，两动点同时停止运动，当时间t为何值时，以Q、O、C为顶点的三角形与△PCO相似？

科目：czsx 来源： 题型：填空题

科目：czsx 来源：2010年浙江省杭州市萧山区中考数学模拟试卷16（城南初中 倪海峰 董正丹）（解析版） 题型：填空题

已知：如图，在直角坐标系中，⊙C与y轴相切于点O，且C点的坐标为（1，0），直线l过点A（-1，0）与⊙C切于D点．D点坐标为    ，在直线l上存在点P，使△APC为等腰三角形，则P点的坐标    ．

科目：czsx 来源： 题型：

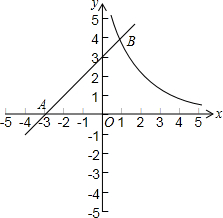
如图，已知直线y=x+3与x轴交于点A，与反比例函数y=

k

x

在第一象限的图象交于点B．如果将直线AB绕点A顺时针旋转15°得到直线l，直线l与y轴交于点C．若点B的横坐标为1，求反比例函数y=

k

x

和直线l的解析式．

科目：czsx 来源： 题型：

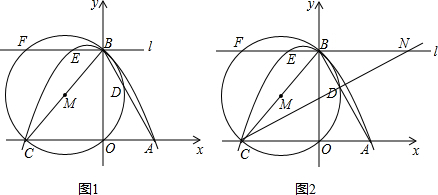
（2013•济南）如图1，抛物线y=-

2

3

x²+bx+c与x轴相交于点A，C，与y轴相交于点B，连接AB，BC，点A的坐标为（2，0），tan∠BAO=2，以线段BC为直径作⊙M交AB与点D，过点B作直线l∥AC，与抛物线和⊙M的另一个交点分别是E，F．
（1）求该抛物线的函数表达式；
（2）求点C的坐标和线段EF的长；
（3）如图2，连接CD并延长，交直线l于点N，点P，Q为射线NB上的两个动点（点P在点Q的右侧，且不与N重合），线段PQ与EF的长度相等，连接DP，CQ，四边形CDPQ的周长是否有最小值？若有，请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值；若没有，请说明理由．

科目：czsx 来源： 题型：

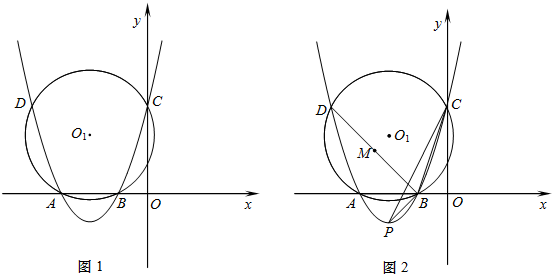
（2012•济南）如图1，抛物线y=ax²+bx+3与x轴相交于点A（-3，0），B（-1，0），与y轴相交于点C，⊙O₁为△ABC的外接圆，交抛物线于另一点D．
（1）求抛物线的解析式；
（2）求cos∠CAB的值和⊙O₁的半径；
（3）如图2，抛物线的顶点为P，连接BP，CP，BD，M为弦BD中点，若点N在坐标平面内，满足△BMN∽△BPC，请直接写出所有符合条件的点N的坐标．

科目：czsx 来源： 题型：

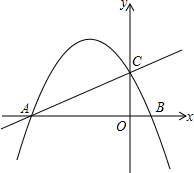
如图，已知直线y=

2

5

x+2与x轴交于点A，交y轴于C．抛物线y=ax²+4ax+b经过A、C两点，抛物线交x轴于另一点B．
（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使△BPC的内心在y轴上？若存在，求出点P的坐标；若不存在，请说明理由；
（3）点Q在抛物线上，且有△AQC和△BQC面积相等，求点Q的坐标．