在梯形ABCD中，AB∥CD，AB=2CD，M、N分别为CD、BC的中点，若 AB =λ AM +μ AN ，则λ+μ=答案解析

科目：gzsx 来源： 题型：

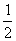
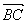
如下图，在梯形ABCD中，=a，=b，=c,=d,E、F分别为AB、CD的中点，则下列表达中成立的是（    ）

A.=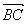（a+b+c+d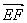）                   B.=（c+d-a-b）

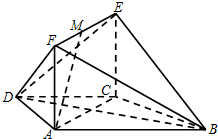
C.=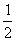（a+b-c-d）                     D.=（a-b+c-d）

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
（Ⅰ）求证：BC⊥平面ACFE；．
（Ⅱ）求二面角B-EF-D的平面角的余弦值．

科目：gzsx 来源： 题型：

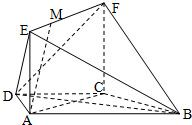
如图，在梯形ABCD中，AB∥CD，AB=4，CD=2．E，F分别为AD，BC上点，且EF=3，EF∥AB，则梯形ABFE与梯形EFCD的面积比为

 

．

科目：gzsx 来源： 题型：

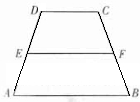
如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
（Ⅰ）求证：BC⊥平面ACFE；
（Ⅱ）当EM为何值时，AM∥平面BDF？证明你的结论．

科目：gzsx 来源： 题型：

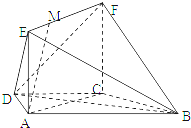
如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
（1）求证：BC⊥平面ACFE；
（2）当EM为何值时，AM∥平面BDF？证明你的结论；
（3）求二面角B-EF-D的平面角的余弦值．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

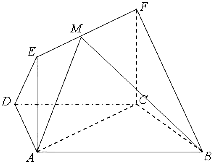
如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
（Ⅰ）求证：BC⊥平面ACFE；
（Ⅱ）点M在线段EF上运动，设平面MAB与平面FCB所成二面角的平面角为θ（θ≤90°），试求cosθ的取值范围．

科目：gzsx 来源： 题型：

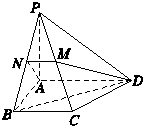
如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点．
（Ⅰ）求证：PB⊥DM；
（Ⅱ）求CD与平面ADMN所成的角．

科目：gzsx 来源： 题型：

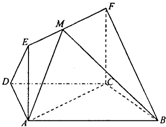
如图，在梯形△ABCD中，AB∥CD，AD=DC-=CB=1，么ABC-60．，四边形ACFE为矩形，平面ACFE上平面ABCD，CF=1．
（I）求证：BC⊥平面ACFE；
（II）若M为线段EF的中点，设平面MAB与平面FCB所成二面角的平面角为θ（θ≤90°），求cosθ．

科目：gzsx 来源： 题型：

如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
（1）求证：BC⊥平面ACFE；
（2）当EM为何值时，AM∥平面BDF？写出结论，并加以证明．
（3）当EM为何值时，AM⊥BE？写出结论，并加以证明．

科目：gzsx 来源： 题型：

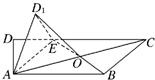
如图，在梯形ABCD中，AB∥CD，∠ADC=90°，3AD=DC=3，AB=2，E是DC上点，且满足DE=1，连接AE，将△DAE沿AE折起到△D₁AE的位置，使得∠D₁AB=60°，设AC与BE的交点为O．
（1）试用基向量

AB

，

AE

，

AD1

表示向量

OD1

；
（2）求异面直线OD₁与AE所成角的余弦值；
（3）判断平面D₁AE与平面ABCE是否垂直？并说明理由．

科目：gzsx 来源： 题型：

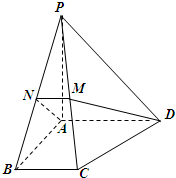
（2013•广州三模）如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，PA=AD=AB=2BC，M，N分别为PC，PB的中点．
（Ⅰ）求证：PB⊥DM；
（Ⅱ）求CD与平面ADMN所成的角的正弦值．

科目：gzsx 来源： 题型：

（2012•江西）如图，在梯形ABCD中，AB∥CD，E，F是线段AB上的两点，且DE⊥AB，CF⊥AB，AB=12，AD=5，BC=4

2

，DE=4．现将△ADE，△CFB分别沿DE，CF折起，使A，B两点重合与点G，得到多面体CDEFG．
（1）求证：平面DEG⊥平面CFG；
（2）求多面体CDEFG的体积．

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

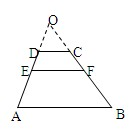
如图，在梯形ABCD中，AB∥CD，AB=a，CD=b（a＞b）．若EF∥AB，EF到CD与AB的距离之比为m：n，则可推算出：EF=

ma+nb

m+n

，用类比的方法，推想出下列问题的结果，在上面的梯形ABCD中，延长梯形的两腰AD和BC交于O点，设△OAB，△OCD的面积分别为S₁，S₂，EF∥AB，，且EF到CD与AB的距离之比为m：n，则△OEF的面积S₀与S₁，S₂的关系是（　　）

A．S0= mS1+nS2 m+n	B．S0= nS1+mS2 m+n
C． S0 = m S1 +n S2 m+n	D． S0 = n S1 +m S2 m+n

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

科目：gzsx 来源： 题型：

（2013•绍兴一模）如图，在梯形ABCD中，AB∥CD，AB⊥AD，AD=4，点P在平面ABCD上的射影中点O，且PA=PD=2

3

，二面角P-AD-B为45°．
（1）求直线OA与平面PAB所成角的大小；
（2）若AB+BP=8求三棱锥P-ABD的体积．

科目：gzsx 来源： 题型：

如图，在梯形ABCD中，AB∥DC，AB=a，CD=b（a＞b）．若EF∥AB，EF到CD与AB的距离之比为m：n，则可推算出：EF=

ma+nb

m+n

．试用类比的方法，推想出下述问题的结果．在上面的梯形ABCD中，延长梯形两腰AD，BC相交于O点，设△OAB，△OCD的面积分别为S₁，S₂，EF∥AB且EF到CD与AB的距离之比为m：n，则△OEF的面积S₀与S₁，S₂的关系是

S0

=

m S1 +n S2

m+n

S0

=

m S1 +n S2

m+n

．