如图，在△ABC中，∠ACB=90°∠B=45°答案解析

科目：czsx 来源： 题型：

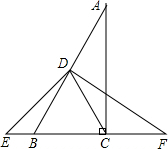
已知：如图，在△ABC中，∠ACB=90°点D是AB的中点，延长BC到点F，延长CB到点E，使CF=BE，连接DE、DC、DF．
求证：DE=DF．

科目：czsx 来源： 题型：

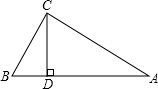
已知：如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为点D，若∠A=30°，CD=6，则AB的长是

8

3

8

3

．

科目：czsx 来源： 题型：

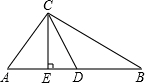
如图，在△ABC中，∠ACB=90°，∠B=30°，CD，CE分别是AB边上的中线和高．
（1）求证：AE=ED；
（2）若AC=2，求△CDE的周长．

科目：czsx 来源： 题型：

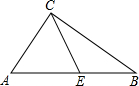
如图，在△ABC中，∠ACB=90°，AC=8m，BC=6m，E是AB边的中点，则CE的长是

 

．

科目：czsx 来源： 题型：

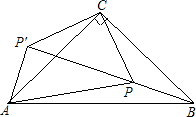
如图，在△ABC中，∠ACB=90°，AC=BC，点P在△ABC内，△AP′C是由△BPC绕着点C旋转得到的，PA=

5

，PB=1，∠BPC=135°．则PC=

 

．

科目：czsx 来源： 题型：

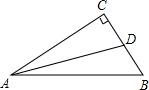
如图，在△ABC中，∠ACB=90°，AD是△ABC角平分线，且AB=10，AC=8，那么，△ABD与△ACD面积的比值是

5：4

5：4

．

科目：czsx 来源： 题型：

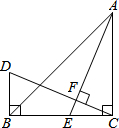
如图，在△ABC中，∠ACB=90°，AC=BC，E是BC上的一点，过点C作CF⊥AE于F，过B作BD⊥CB交CF的延长线于点D．
（1）求证：AE=CD；
（2）若BD=5cm，BC=12cm，求CF的长．

科目：czsx 来源： 题型：

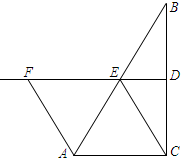
如图，在△ABC中，∠ACB=90°，BC的垂直平分线DE交BC于D，交AB于E，F在射线DE上，并且EF=AC．
（1）求证：AF=CE；
（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论；
（3）四边形ACEF有可能是正方形吗？为什么？

科目：czsx 来源： 题型：

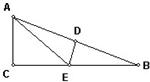
10、如图，在△ABC中，∠ACB=90°，DE是AB的垂直平分线，∠CAE：∠EAB=4：1．则∠B的度数为（　　）度．

A、15°

B、20°

C、30°

D、45°

科目：czsx 来源： 题型：

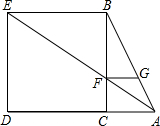
已知：如图，在△ABC中，∠ACB=90°，以BC为边向外作正方形BEDC，连接AE交BC于F，作FG∥BE交AB于G，求证：FG=FC．

科目：czsx 来源： 题型：

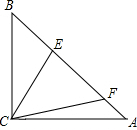
（2013•思明区一模）如图，在△ABC中，∠ACB=90°，CB=CA=

2

，点E、F在线段AB上（不与端点A、B重合），且∠ECF=45°．
（1）求证：BF•AE=2；
（2）判断BE、EF、FA三条线段所组成的三角形的形状，并说明理由．

科目：czsx 来源： 题型：

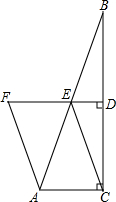
（2012•门头沟区一模）已知：如图，在△ABC中，∠ACB=90°，点E为AB的中点，过点E作ED⊥BC于D，F在DE的延长线上，且AF=CE，若AB=6，AC=2，求四边形ACEF的面积．

科目：czsx 来源： 题型：

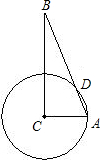
如图，在△ABC中，∠ACB=90°，∠B=15°，以C为圆心，CA为半径的圆交AB于D点，若AC=6，求弧AD的长．

科目：czsx 来源： 题型：

如图，在△ABC中，∠ACB=90°，AC=BC，D是AB上的点且AD=

1

3

BD，如果CD=kAD，那么k等于（　　）

A． 3

B．2

C． 5

D．2

科目：czsx 来源： 题型：

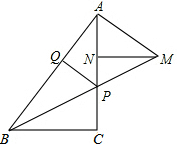
如图，在△ABC中，∠ACB=90゜，P为AC上一点，PQ⊥AB于Q，AM⊥AB交BP的延长线于M，MN⊥AC于N，AQ=MN．
（1）求证：AP=AM；
（2）求证：PC=AN．

科目：czsx 来源： 题型：

如图，在△ABC中，∠ACB=90°，AC=BC，点D为AB的中点，AE=CF．求证：DE⊥DF．

科目：czsx 来源： 题型：

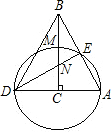
如图，在△ABC中，∠ACB=90°，以C为圆心、CA的长为半径的圆分别交AB、CB于E、M，AC的延长线交⊙C于D，连接DE交CB于N，连接BD．求证：
（1）△ABD是等腰三角形；
（2）CM²=CN•CB．

科目：czsx 来源： 题型：

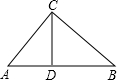
如图，在△ABC中，∠ACB=90°，CD⊥AB于D，AC=

3

，BC=

6

，求：sin∠BCD、cos∠BCD和tan∠BCD的值．

科目：czsx 来源： 题型：

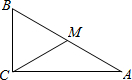
（2012•闸北区二模）如图，在△ABC中，∠ACB=90°，∠A=30°，BC=2，点M是斜边AB的中点，那么CM=

2

2

．

科目：czsx 来源： 题型：

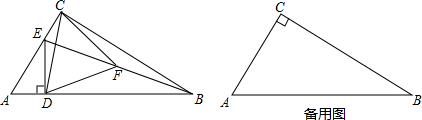
如图，在△ABC中，∠ACB=90°，∠A=60°，AC=3，点D是边AB上的动点（点D与点A、B不重合），过点D作DE⊥AB交射线AC于E，连接BE，点F是BE的中点，连接CD、CF、DF．
（1）当点E在边AC上（点E与点C不重合）时，设AD=x，CE=y．
①直接写出y关于x的函数关系式及定义域；
②求证：△CDF是等边三角形；
（2）如果BE=2

7

，请直接写出AD的长．