科目:gzsx
来源:《圆锥曲线》2012-2013学年广东省十三大市高三(上)期末数学试卷汇编(理科)(解析版)
题型:解答题
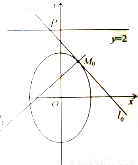
如图,已知点M
(x
,y
)是椭圆C:

=1上的动点,以M
为切点的切线l
与直线y=2相交于点P.
(1)过点M
且l
与垂直的直线为l
1,求l
1与y轴交点纵坐标的取值范围;
(2)在y轴上是否存在定点T,使得以PM
为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.
(参考定理:若点Q(x
1,y
1)在椭圆

,则以Q为切点的椭圆的切线方程是:
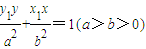
.
查看答案和解析>>
科目:gzsx
来源:2013年广东省湛江市高考数学一模试卷(理科)(解析版)
题型:解答题
如图,已知点M
(x
,y
)是椭圆C:
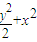
=1上的动点,以M
为切点的切线l
与直线y=2相交于点P.
(1)过点M
且l
与垂直的直线为l
1,求l
1与y轴交点纵坐标的取值范围;
(2)在y轴上是否存在定点T,使得以PM
为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.
(参考定理:若点Q(x
1,y
1)在椭圆
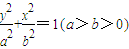
,则以Q为切点的椭圆的切线方程是:

.

查看答案和解析>>
科目:gzsx
来源:2013年广东省高考数学押题预测试卷(理科)(解析版)
题型:解答题
如图,已知点M
(x
,y
)是椭圆C:

=1上的动点,以M
为切点的切线l
与直线y=2相交于点P.
(1)过点M
且l
与垂直的直线为l
1,求l
1与y轴交点纵坐标的取值范围;
(2)在y轴上是否存在定点T,使得以PM
为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.
(参考定理:若点Q(x
1,y
1)在椭圆

,则以Q为切点的椭圆的切线方程是:
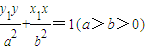
.

查看答案和解析>>
科目:gzsx
来源:
题型:
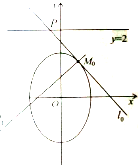
(2013•湛江一模)如图,已知点M
0(x
0,y
0)是椭圆C:
+x2=1上的动点,以M
0为切点的切线l
0与直线y=2相交于点P.
(1)过点M
0且l
0与垂直的直线为l
1,求l
1与y轴交点纵坐标的取值范围;
(2)在y轴上是否存在定点T,使得以PM
0为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,说明理由.
(参考定理:若点Q(x
1,y
1)在椭圆
+=1(a>b>0),则以Q为切点的椭圆的切线方程是:
+=1(a>b>0).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为
,又椭圆上任一点到两焦点的距离和为
2,过点M(0,
-)与x轴不垂直的直线l交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:2013年湖北新洲、红安、麻城一中高三上学期期末考文科数学试卷(解析版)
题型:解答题
(本小题满分14分)
已知椭圆的中心是坐标原点 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为 ,过点M(0,
,过点M(0,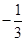 )与x轴不垂直的直线
)与x轴不垂直的直线 交椭圆于P、Q两点.
交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为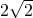 ,过点M(0,
,过点M(0,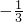 )与x轴不垂直的直线l交椭圆于P、Q两点.
)与x轴不垂直的直线l交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年湖北省新洲一中、红安一中、麻城一中高三(上)期末数学试卷(文科)(解析版)
题型:解答题
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为
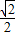
,又椭圆上任一点到两焦点的距离和为
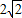
,过点M(0,

)与x轴不垂直的直线l交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为
,又椭圆上任一点到两焦点的距离和为
2,过点M(0,
-)与x轴不垂直的直线l交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
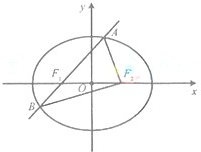
(2012•福建)如图,椭圆E:
+ =1(a>b>0)的左焦点为F
1,右焦点为F
2,离心率e=
.过F
1的直线交椭圆于A、B两点,且△ABF
2的周长为8.
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知动圆P(圆心为点P)过定点A(1,0),且与直线x=-1相切,记动点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点P的直线l与曲线C相切,且与直线x=-1相交于点Q.试研究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
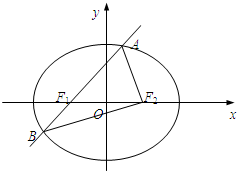
(2013•崇明县一模)如图,椭圆
E:+=1(a>b>0)的左焦点为F
1,右焦点为F
2,过F
1的直线交椭圆于A,B两点,△ABF
2的周长为8,且△AF
1F
2面积最大时,△AF
1F
2为正三角形.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系?
②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:2014届北京市西城区高二上学期期末考试文科数学试卷(解析版)
题型:解答题
(本小题满分14分)
已知动圆P(圆心为点P)过定点A(1,0),且与直线 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。
(Ⅰ)求轨迹C的方程;
(Ⅱ)设过点P的直线l与曲线C相切,且与直线 相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。
相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。
查看答案和解析>>
科目:gzsx
来源:2012年全国普通高等学校招生统一考试理科数学(福建卷解析版)
题型:解答题
如图,椭圆E: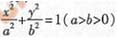 的左焦点为F1,右焦点为F2,离心率
的左焦点为F1,右焦点为F2,离心率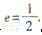 。过F1的直线交椭圆于A、B两点,且△ABF2的周长为8
。过F1的直线交椭圆于A、B两点,且△ABF2的周长为8
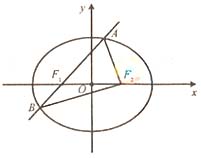
(Ⅰ)求椭圆E的方程。
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q。试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由
【解析】
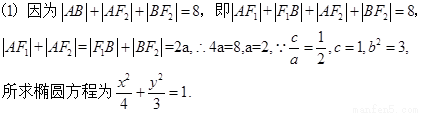

查看答案和解析>>
科目:gzsx
来源:2012-2013学年北京市西城区(北区)高二(上)期末数学试卷(理科)(解析版)
题型:解答题
已知动圆P(圆心为点P)过定点A(1,0),且与直线x=-1相切,记动点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点P的直线l与曲线C相切,且与直线x=-1相交于点Q.试研究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:2012年福建省高考数学试卷(理科)(解析版)
题型:解答题
如图,椭圆E:

的左焦点为F
1,右焦点为F
2,离心率e=

.过F
1的直线交椭圆于A、B两点,且△ABF
2的周长为8.
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
已知动圆P(圆心为点P)过定点A(1,0),且与直线x=-1相切,记动点P的轨迹为C.
(1)求轨迹C的方程;
(2)设过点P的直线l与曲线C相切,且与直线x=-1相交于点Q.试研究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
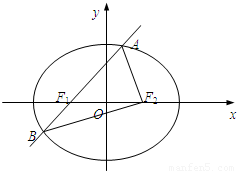
来源:2013年上海市崇明县高考数学一模试卷(文科)(解析版)
题型:解答题
如图,椭圆

的左焦点为F
1,右焦点为F
2,过F
1的直线交椭圆于A,B两点,△ABF
2的周长为8,且△AF
1F
2面积最大时,△AF
1F
2为正三角形.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系?
②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
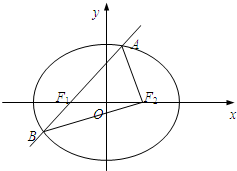 如图,椭圆
如图,椭圆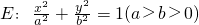 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系?
②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年福建省三明一中高二(上)期中数学试卷(理科)(解析版)
题型:解答题
如图,椭圆E:

的左焦点为F
1,右焦点为F
2,离心率e=

.过F
1的直线交椭圆于A、B两点,且△ABF
2的周长为8.
(Ⅰ)求椭圆E的方程.
(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>

 =1上的动点,以M为切点的切线l与直线y=2相交于点P.
=1上的动点,以M为切点的切线l与直线y=2相交于点P. ,则以Q为切点的椭圆的切线方程是:
,则以Q为切点的椭圆的切线方程是: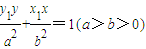 .
.
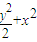 =1上的动点,以M为切点的切线l与直线y=2相交于点P.
=1上的动点,以M为切点的切线l与直线y=2相交于点P.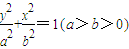 ,则以Q为切点的椭圆的切线方程是:
,则以Q为切点的椭圆的切线方程是: .
.
 =1上的动点,以M为切点的切线l与直线y=2相交于点P.
=1上的动点,以M为切点的切线l与直线y=2相交于点P. ,则以Q为切点的椭圆的切线方程是:
,则以Q为切点的椭圆的切线方程是: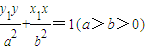 .
.
 (2013•湛江一模)如图,已知点M0(x0,y0)是椭圆C:
(2013•湛江一模)如图,已知点M0(x0,y0)是椭圆C: ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为 ,过点M(0,
,过点M(0,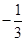 )与x轴不垂直的直线
)与x轴不垂直的直线 交椭圆于P、Q两点.
交椭圆于P、Q两点. ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为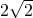 ,过点M(0,
,过点M(0,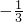 )与x轴不垂直的直线l交椭圆于P、Q两点.
)与x轴不垂直的直线l交椭圆于P、Q两点.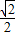 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为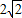 ,过点M(0,
,过点M(0, )与x轴不垂直的直线l交椭圆于P、Q两点.
)与x轴不垂直的直线l交椭圆于P、Q两点. (2012•福建)如图,椭圆E:
(2012•福建)如图,椭圆E: (2013•崇明县一模)如图,椭圆E:
(2013•崇明县一模)如图,椭圆E: 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。 相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。
相交于点Q。试研究:在x轴上是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。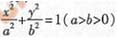 的左焦点为F1,右焦点为F2,离心率
的左焦点为F1,右焦点为F2,离心率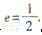 。过F1的直线交椭圆于A、B两点,且△ABF2的周长为8
。过F1的直线交椭圆于A、B两点,且△ABF2的周长为8
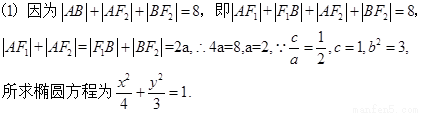

 的左焦点为F1,右焦点为F2,离心率e=
的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
 如图,椭圆
如图,椭圆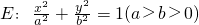 的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1,右焦点为F2,过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形. 的左焦点为F1,右焦点为F2,离心率e=
的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.