科目:gzsx 来源:同步题 题型:单选题
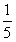
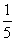 <a<1
<a<1 科目:gzsx 来源:2008-2009学年江苏省盐城市东台市高三(上)期末数学试卷(文科)(解析版) 题型:选择题
科目:gzsx 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
科目:gzsx 来源:2011年宁夏石嘴山十三中高考数学模拟试卷(解析版) 题型:选择题

 <a<1
<a<1科目:gzsx 来源:不详 题型:单选题
| A.-1<a<1 | B.0<a<1 | C.-1<a<
| D.-
|
科目:gzsx 来源:海南省期中题 题型:单选题
[ ]

 <a<1
<a<1 科目:gzsx 来源: 题型:
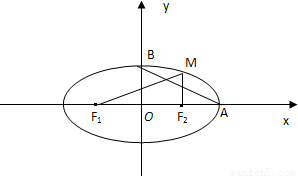
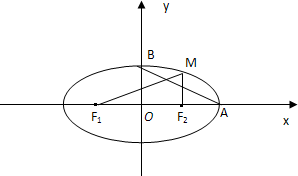 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 3 |
| π |
| 2 |
科目:gzsx 来源:2012-2013学年浙江省宁波市余姚中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
科目:gzsx 来源:2012-2013学年浙江省宁波市余姚中学高二(上)期中数学试卷(理科)(解析版) 题型:填空题
科目:gzsx 来源:2011年上海市崇明县高考数学二模试卷(理科)(解析版) 题型:解答题
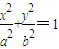 (a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为
(a>b>0),M为椭圆上的一个动点,F1、F2分别为椭圆的左、右焦点,A、B分别为椭圆的一个长轴端点与短轴的端点.当MF2⊥F1F2时,原点O到直线MF1的距离为 |OF1|.
|OF1|.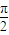 ;
;