四棱柱ABCD-A1B1C1D1的三视图如下 求证D1C⊥AC1答案解析
科目:gzsx
来源:2012届河北冀州中学高二年级下学期第三次月考题(文)
题型:解答题
四棱柱ABCD—A1B1C1D1的三视图和直观图如下
(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.


查看答案和解析>>
科目:gzsx
来源:2010-2011学年河北冀州中学高二年级下学期第三次月考题(文)
题型:解答题
四棱柱ABCD—A1B1C1D1的三视图和直观图如下
(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.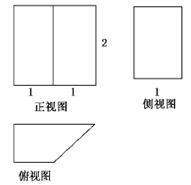
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正四棱柱ABCD-A
1B
1C
1D
1的顶点坐标分别为A(0,0,0),B(2,0,O),D(0,2,0),A
1(0,0,5),则C
1的坐标为
(2,2,5)
(2,2,5)
.
查看答案和解析>>
科目:gzsx
来源:
题型:
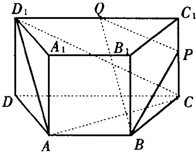
如图,直四棱柱ABCD-A
1B
1C
1D
1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD
1=AB=1,
P、Q分别是CC
1、C
1D
1的中点.点P到直线AD
1的距离为
.
(1)求证:AC∥平面BPQ;
(2)求二面角B-PQ-D的大小.
查看答案和解析>>
科目:gzsx
来源:
题型:
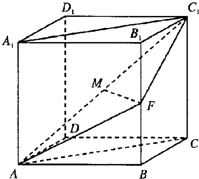
已知直四棱柱ABCD-A
1B
1C
1D
1的底面是菱形,且∠DAB=60°,AD=AA
1,F为棱BB
1的中点,M为线段AC
1的中点.
(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC
1⊥平面ACC
1A
1;
(3)求平面AFC
1与平面ABCD所成二面角的大小.
查看答案和解析>>
科目:gzsx
来源:
题型:

(2013•黄冈模拟)如图,在四棱柱ABCD-A
1B
1C
1D
1中,已 知平面AA
1C
1C丄平面ABCD,且AB=BC=CA=
,AD=CD=1
(I)求证:BD丄AA
1;
(II)若四边形ACC
1A
1是菱形,且∠A
1AC=60°,求四棱柱 ABCD-A
1B
1C
1D
1 的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知正四棱柱ABCD-A
1B
1C
1D
1的底面ABCD边长为1,高AA
1=
,它的八个顶点都在同一球面上,那么球的半径是
;A,B两点的球面距离为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
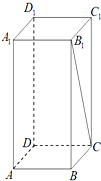
如图,正四棱柱ABCD-A
1B
1C
1D
1的底面边长AB=2,若直线B
1C与底面ABCD所成的角的大小为arctan2,则正四棱柱ABCD-A
1B
1C
1D
1的侧面积为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
正四棱柱ABCD-A
1B
1C
1D
1的底面边长为1,高为2,一直径为1的球O恰与底面ABCD及四个侧面都相切,直线AC
1与球O交于MN两点,则MN的长为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
若正四棱柱ABCD-A
1B
1C
1D
1的底面边长为1,AB
1与底面ABCD成60°角,则A
1C
1到底面ABCD的距离为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
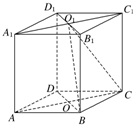
如图,直四棱柱ABCD-A
1B
1C
1D
1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A
1C
1∩B
1D
1=O
1,则二面角O
1-BC-D的大小为
60°
60°
.
查看答案和解析>>
科目:gzsx
来源:
题型:
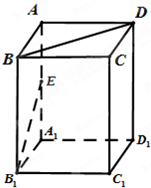
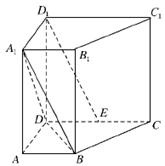
已知四棱柱ABCD-A
1B
1C
1D
1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA
1=2,E是侧棱AA
1的中点,求
(1)求异面直线BD与B
1E所成角的大小;
(2)求四面体AB
1D
1C的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:

(2013•黄浦区二模)已知正四棱柱ABCD-A
1B
1C
1D
1的底面边长为2,且
A1D=.
(1)求该正四棱柱的体积;
(2)若E为线段A
1D的中点,求异面直线BE与AA
1所成角的大小.
查看答案和解析>>
科目:gzsx
来源:
题型:

已知ABCD-A
1B
1C
1D
1是底面边长1正四棱柱,O
1为A
1C
1与B
1D
1的交点.
(1)设AB
1与底面A
1B
1C
1D
1所成的角为
arctan,求该棱柱的侧面积;
(2)(理)若点C到平面AB
1D
1的距离为
,求四棱柱ABCD-A
1B
1C
1D
1的体积.
(3)(文)设高AA
1=2,求四面体AB
1D
1C的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
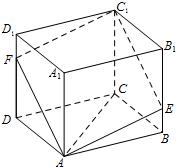
(2012•深圳二模)如图,四棱柱ABCD-A
1B
1C
1D
1的底面ABCD是平行四边形,E,F分别在棱BB
1,DD
1上,且AF∥EC
1.
(1)求证:AE∥FC
1;
(2)若AA
1⊥平面ABCD,四边形AEC
1F是边长为
的正方形,且BE=1,DF=2,求线段CC
1的长,并证明:AC⊥EC
1.
查看答案和解析>>
科目:gzsx
来源:
题型:
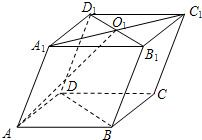
18、如图,四棱柱ABCD-A
1B
1C
1D
1的底面边长和侧棱长均为1,∠BAD=∠BAA
1=∠DAA
1=60°,O
1为A
1C
1中点.
求证:AO
1∥平面C
1BD.
查看答案和解析>>
科目:gzsx
来源:
题型:
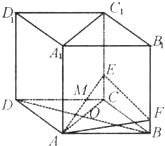
已知直四棱柱ABCD-A
1B
1C
1D
1的底面是菱形AC∩BD=0,AB=2,∠ABC=60°,E、F分别为棱CC
1,BB
1上的点,EC=BC=2FB,M是AE的中点.
(1) 求证:FM∥BO(2) 求三棱锥E-ABD的体积.
查看答案和解析>>
科目:gzsx
来源:
题型:
正四棱柱ABCD-A
1B
1C
1D
1的体积为4
,高为
,则点A
1到平面BDC
1的距离为( )
查看答案和解析>>
科目:gzsx
来源:
题型:
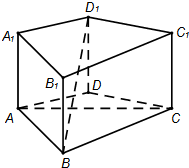
(2013•泉州模拟)如图,四棱柱ABCD-A
1B
1C
1D
1中,AA
1⊥平面ABCD.
(Ⅰ)从下列①②③三个条件中选择一个做为AC⊥BD
1的充分条件,并给予证明;
①AB⊥BC,②AC⊥BD;③ABCD是平行四边形.
(Ⅱ)设四棱柱ABCD-A
1B
1C
1D
1的所有棱长都为1,且∠BAD为锐角,求平面BDD
1与平面BC
1D
1所成锐二面角θ的取值范围.
查看答案和解析>>
科目:gzsx
来源:
题型:
正四棱柱ABCD-A1B1C1D1的上底面ABCD的四个顶点在球面上,下底面A1B1C1D1过球心O,且正四棱柱的底面边长为2,高为1,则球0的表面积为( )
查看答案和解析>>





 如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1,
如图,直四棱柱ABCD-A1B1C1D1的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD1=AB=1, 已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1的中点,M为线段AC1的中点. (2013•黄冈模拟)如图,在四棱柱ABCD-A1B1C1D1中,已 知平面AA1C1C丄平面ABCD,且AB=BC=CA=
(2013•黄冈模拟)如图,在四棱柱ABCD-A1B1C1D1中,已 知平面AA1C1C丄平面ABCD,且AB=BC=CA= 如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若直线B1C与底面ABCD所成的角的大小为arctan2,则正四棱柱ABCD-A1B1C1D1的侧面积为
如图,正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若直线B1C与底面ABCD所成的角的大小为arctan2,则正四棱柱ABCD-A1B1C1D1的侧面积为 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为 已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求
已知四棱柱ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,AA1=2,E是侧棱AA1的中点,求 (2013•黄浦区二模)已知正四棱柱ABCD-A1B1C1D1的底面边长为2,且A1D=
(2013•黄浦区二模)已知正四棱柱ABCD-A1B1C1D1的底面边长为2,且A1D= 已知ABCD-A1B1C1D1是底面边长1正四棱柱,O1为A1C1与B1D1的交点.
已知ABCD-A1B1C1D1是底面边长1正四棱柱,O1为A1C1与B1D1的交点. (2012•深圳二模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1.
(2012•深圳二模)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,E,F分别在棱BB1,DD1上,且AF∥EC1. 18、如图,四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,O1为A1C1中点.
18、如图,四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,O1为A1C1中点. 已知直四棱柱ABCD-A1B1C1D1的底面是菱形AC∩BD=0,AB=2,∠ABC=60°,E、F分别为棱CC1,BB1上的点,EC=BC=2FB,M是AE的中点.
已知直四棱柱ABCD-A1B1C1D1的底面是菱形AC∩BD=0,AB=2,∠ABC=60°,E、F分别为棱CC1,BB1上的点,EC=BC=2FB,M是AE的中点. (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.