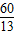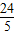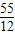科目:czsx
来源:
题型:
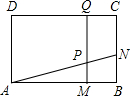
如图,矩形ABCD,AD=3厘米,AB=4厘米,N为BC上一点,BN=1厘米,动点M从B点出发,沿BA运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于点P,Q.当点M到达终点A时停止运动.设运
动时间为t秒.
(1)若t=1秒,则PM=
厘米;
(2)设四边形PNCQ的面积为S,求S与t的函数关系式;
(3)M运动到什么位置时,四边形PNCQ的面积与矩形ABCD的面积的比为9:24?
查看答案和解析>>
科目:czsx
来源:
题型:

如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
(1)找出图中一对全等三角形;(△ABD≌△CDB除外)
(2)求证:BE=DE;
(3)求BE的长.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
(1)找出图中一对全等三角形;(△ABD≌△CDB除外)
(2)求证:BE=DE;
(3)求BE的长.
查看答案和解析>>
科目:czsx
来源:2010-2011学年上海市市北中学九年级(上)月考数学试卷(11月份)(解析版)
题型:解答题
如图,矩形ABCD,AD=3厘米,AB=4厘米,N为BC上一点,BN=1厘米,动点M从B点出发,沿BA运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于点P,Q.当点M到达终点A时停止运动.设运动时间为t秒.
(1)若t=1秒,则PM=______厘米;
(2)设四边形PNCQ的面积为S,求S与t的函数关系式;
(3)M运动到什么位置时,四边形PNCQ的面积与矩形ABCD的面积的比为9:24?

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,矩形ABCD,AD=3厘米,AB=4厘米,N为BC上一点,BN=1厘米,动点M从B点出发,沿BA运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于点P,Q.当点M到达终点A时停止运动.设运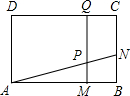 动时间为t秒.
动时间为t秒.
(1)若t=1秒,则PM=________厘米;
(2)设四边形PNCQ的面积为S,求S与t的函数关系式;
(3)M运动到什么位置时,四边形PNCQ的面积与矩形ABCD的面积的比为9:24?
查看答案和解析>>
科目:czsx
来源:
题型:
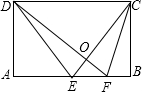
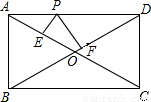
如图:矩形ABCD中,E是AB的中点,2AD=AB,F是BE的中点.若AD=5,那么△OCD的面积是
20
20
.
查看答案和解析>>
科目:czsx
来源:
题型:
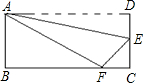
(2012•黔东南州)如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )
查看答案和解析>>
科目:czsx
来源:
题型:
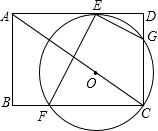
如图,矩形ABCD,AD=8,DC=6,在对角线AC上取一点O,以OC为半径的圆切AD于E,交BC于F,交CD于G.
(1)求⊙O的半径R;
(2)设∠BFE=α,∠CED=β,请写出α,β,90°三者之间的关系式(只需写出一个)并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
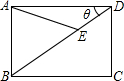
如图,矩形ABCD(AD>AB)中,AB=α,∠BDA=θ作AE交BD于E,且AE=AB,试用α和θ表示AD和BE的长.
查看答案和解析>>
科目:czsx
来源:
题型:
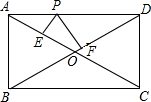
如图,矩形ABCD中,已知AB=5,AD=12,P是AD上的动点,PE⊥AC,E,PF⊥BD于F,则PE+PF=( )
查看答案和解析>>
科目:czsx
来源:
题型:
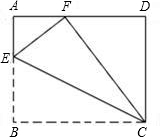
如图,矩形ABCD纸片,E是AB上的一点,且BE:EA=5:3,CE=15
,把△BCE沿折痕EC向上翻折,若点B恰好与AD边上的点F重合,求AB、BC的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,矩形ABCD(AD>AB)中AB=a,∠BDA=θ,作AE交BD于E,且AE=AB,试用a与θ表示:AD=
,BE=
.
查看答案和解析>>
科目:czsx
来源:2013-2014学年浙江杭州萧山党湾镇初中九年级12月质量检测数学试卷(解析版)
题型:解答题
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为弧AB,最后一张纸CD对应为弧CD(CD为半圆),

(1)连结OB,求钝角∠AOB
(2)如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长.
查看答案和解析>>
科目:czsx
来源:2013-2014学年浙江杭州翠苑中学九年级上学期10月质量检测数学试卷(解析版)
题型:解答题
如图,矩形ABCD为一本书,AB=12π,AD=2,当把书卷起时大致如图所示的半圆状(每张纸都是以O为圆心的同心圆的弧),如第一张纸AB对应为 ,最后一张纸CD对应为
,最后一张纸CD对应为 (
( 为半圆),
为半圆),

(1)连结OB,求钝角∠AOB=
;
(2)如果该书共有100张纸,求第40张纸对应的弧超出半圆部分的长.
查看答案和解析>>
科目:czsx
来源:《3.3 平行四边形、矩形、菱形、正方形的性质和判定》2010年第2课时同步练习(解析版)
题型:选择题
如图,矩形ABCD中,已知AB=5,AD=12,P是AD上的动点,PE⊥AC,E,PF⊥BD于F,则PE+PF=( )
A.5
B.
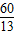
C.
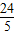
D.
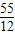
查看答案和解析>>
科目:czsx
来源:2001年全国中考数学试题汇编《四边形》(02)(解析版)
题型:填空题
(2001•杭州)如图,矩形ABCD(AD>AB)中AB=a,∠BDA=θ,作AE交BD于E,且AE=AB,试用a与θ表示:AD=
,BE=
.

查看答案和解析>>
科目:czsx
来源:杭州
题型:填空题
如图,矩形ABCD(AD>AB)中AB=a,∠BDA=θ,作AE交BD于E,且AE=AB,试用a与θ表示:AD=______,BE=______.
查看答案和解析>>
科目:czsx
来源:2001年全国中考数学试题汇编《锐角三角函数》(02)(解析版)
题型:填空题
(2001•杭州)如图,矩形ABCD(AD>AB)中AB=a,∠BDA=θ,作AE交BD于E,且AE=AB,试用a与θ表示:AD=
,BE=
.

查看答案和解析>>
科目:czsx
来源:《21.1 锐角三角函数》2010年同步练习(解析版)
题型:解答题
如图,矩形ABCD(AD>AB)中,AB=α,∠BDA=θ作AE交BD于E,且AE=AB,试用α和θ表示AD和BE的长.

查看答案和解析>>
科目:czsx
来源:2001年全国中考数学试题汇编《圆》(06)(解析版)
题型:解答题
(2001•吉林)如图,矩形ABCD,AD=8,DC=6,在对角线AC上取一点O,以OC为半径的圆切AD于E,交BC于F,交CD于G.
(1)求⊙O的半径R;
(2)设∠BFE=α,∠CED=β,请写出α,β,90°三者之间的关系式(只需写出一个)并证明你的结论.

查看答案和解析>>

 动时间为t秒.
动时间为t秒. 如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处, 如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
如图,矩形ABCD,AD=4,AB=8,沿对角线BD对折,使A点落到点F处,
 动时间为t秒.
动时间为t秒. 如图,矩形ABCD,AD=8,DC=6,在对角线AC上取一点O,以OC为半径的圆切AD于E,交BC于F,交CD于G.
如图,矩形ABCD,AD=8,DC=6,在对角线AC上取一点O,以OC为半径的圆切AD于E,交BC于F,交CD于G. 如图,矩形ABCD中,已知AB=5,AD=12,P是AD上的动点,PE⊥AC,E,PF⊥BD于F,则PE+PF=( )
如图,矩形ABCD中,已知AB=5,AD=12,P是AD上的动点,PE⊥AC,E,PF⊥BD于F,则PE+PF=( ) 如图,矩形ABCD纸片,E是AB上的一点,且BE:EA=5:3,CE=15
如图,矩形ABCD纸片,E是AB上的一点,且BE:EA=5:3,CE=15
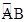 ,最后一张纸CD对应为
,最后一张纸CD对应为 (
( 为半圆),
为半圆),