练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >f

    f答案解析

    科目：gzsx 来源： 题型：

    已知△ABC的面积S满足
    		3
    ≤S≤3
    		3
    ，且
    AB
    •
    BC
    =6    ．
    （1）求角B的取值范围；
    （2）求函数f(B)=
    1-
    		2
    cos(2B-
    π
    4
    )
    sinB
    的值域．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    对于定义域为D的函数y=f（x），若同时满足下列条件：
    ①f（x）在D内单调递增或单调递减；
    ②存在区间[a，b]⊆D，使f（x）在[a，b]上的值域为[a，b]；那么把y=f（x）（x∈D）叫闭函数．
    （1）求闭函数y=-x3符合条件②的区间[a，b]；
    （2）判断函数f(x)=
    3
    4
    x+
    1
    x
      (x＞0)    是否为闭函数？并说明理由；
    （3）若y=k+
    		x+2
    是闭函数，求实数k的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知二次函数f（x）=ax2+bx+c的导数为f′（x），f′（0）＞0，对于任意实数x都有f（x）≥0，则
    f(1)
    f′(0)
    的最小值为（　　）
    A、3
    B、
    5
    2
    C、2
    D、
    3
    2

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=
    		sinx
    +
    		cosx
    ，(0≤x≤
    π
    2
    )    ，则f（x）的值域为
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设
    a
    =(cosx，1)，
    b
    =(sinx，2)
    （1）若
    a
    ∥
    b
    ，求（sinx+cosx）2的值
    （2）若f(x)=(
    a
    -
    b
    )•
    a
    ，求f（x）在[0，π]上的递减区间．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=lg
    kx-1x-1
    ．（k∈R且k＞0）．
    （1）求函数f（x）的定义域；
    （2）若函数f（x）在[10，+∞）上单调递增，求k的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

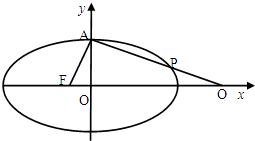    精英家教网设椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
    AP
    =
    8
    5
    PQ
    ．
    （1）求椭圆C的离心率；
    （2）若过A、Q、F三点的圆恰好与直线l：x+
    		3
    y+3=0相切，求椭圆C的方程．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若函数f（x）=sin（3x+φ）的图象关于直线x=
    2π
    3
    对称，则φ的最小正值等于（　　）
    A、
    π
    8
    B、
    π
    4
    C、
    π
    3
    D、
    π
    2

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=(
    1
    2x-1
    +
    1
    2
    )•x    ．
    （1）求函数f（x）的定义域；
    （2）判断函数f（x）的奇偶性；
    （3）求证：f（x）＞0．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    若f(x)=asin(x+
    π
    4
    )+3sin(x-
    π
    4
    )    是偶函数，则a=
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设A（x1，y1），B（x2，y2）是椭圆
    x2
    b2
    +
    y2
    a2
    =1    ，（a＞b＞0）上的两点，已知向量
    m
    =（
    x1
    b
    ，
    y1
    a
    ），
    n
    =（
    x2
    b
    ，
    y2
    a
    ），且
    m
    •
    n
    =0    ，若椭圆的离心率e=
    		3
    2
    ，短轴长为2，O为坐标原点：
    （Ⅰ）求椭圆的方程；
    （Ⅱ）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；
    （Ⅲ）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    12、若f（x）是R上的奇函数，且f（2x-1）的周期为4，若f（6）=-2，则f（2008）+f（2010）=
    2
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    下列命题中：
    ①函数f（x）=sinx+
    2
    sinx
    （x∈（0，π））的最小值是2
    		2
    ；
    ②在△ABC中，若sin2A=sin2B，则△ABC是等腰或直角三角形：
    ③如果正实数a，b，c满足a+b＞c，则
    a
    1+a
    +
    b
    1+b
    ＞
    c
    1+c
    ；其中正确的命题是（　　）
    A、①②③B、①C、②③D、③

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=
    -x2+2x，x＞0
    0，x=0
    x2+mx，x＜0
    是奇函数．
    （1）求实数m的值；
    （2）若函数f（x）在区间[-1，a-2]上单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知f（x）是定义在R上的奇函数，x＞0时，f（x）=x2-2x+3，则f（x）=
     
    ．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

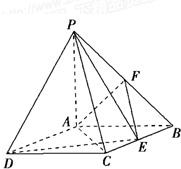    精英家教网如图，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=
    		3
    ，点F是PB的中点，点E在边BC上移动．
    （1）点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
    （2）求证：无论点E在BC边的何处，都有PE⊥AF；
    （3）当BE为何值时，PA与平面PDE所成角的大小为45°？

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=
    2x+2-x
    2
    ，g（x）=
    2x-2-x
    2
    ，
    （1）计算：[f（1）]2-[g（1）]2；
    （2）证明：[f（x）]2-[g（x）]2是定值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知y=f（x）是定义在R上的奇函数，若x＜0时，f（x）=1+2x，求f（x）并画出其图象．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f（x）=x3-ax2-bx+a2，x∈R，a，b为常数．
    （1）若函数f（x）在x=1处有极值10，求实数a，b的值；
    （2）若函数f（x）是奇函数，
    ①方程f（x）=2在x∈[-2，4]上恰有3个不相等的实数解，求实数b的取值范围；
    ②不等式f（x）+2b≥0对∀x∈[1，4]恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知函数f(x)=log2
    1+x
    1-x
    ．
    （1）判断函数f（x）的奇偶性；
    （2）求证f(x1)+f(x2)=f(
    x1+x2
    1+x1x2
    )
    （3）若f(
    a+b
    1+ab
    )=1    ，f(-b)=
    1
    2
    ，求f（a）的值．

    查看答案和解析>>