
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
A.点p关于x轴对称的坐标是p1(x,-y,z)
B.点p关于yOz平面对称的坐标是p2(x,-y,-z)
C.点p关于y轴对称点的坐标是p3(x,-y,z)
D.点p关于原点对称点的坐标是(-x,-y,-z)
科目:gzsx 来源:2012-2013学年湖北省襄阳四中、龙泉中学、荆州中学联考高二(下)期中数学试卷(理科)(解析版) 题型:选择题
 ,则x+y+z=( )
,则x+y+z=( )
科目:gzsx 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
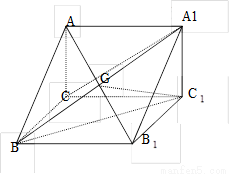
已知直三棱柱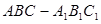 中,
中, 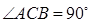 ,
,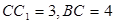 ,
,
 是
是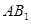 和
和 的交点, 若
的交点, 若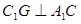 .
.
(1)求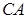 的长; (2)求点
的长; (2)求点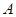 到平面
到平面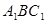 的距离;
的距离;
(3)求二面角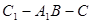 的平面角的正弦值的大小.
的平面角的正弦值的大小.
【解析】本试题主要考查了距离和角的求解运用。第一问中,利用ACC A
A 为正方形,
为正方形,  AC=3
AC=3
第二问中,利用面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD=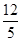 ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为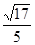
解法一: (1)连AC 交A
交A C于E, 易证ACC
C于E, 易证ACC A
A 为正方形,
为正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD=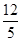 … 8分
… 8分
(3) 易得AC
 面A
面A CB,
过E作EH
CB,
过E作EH A
A B于H, 连HC
B于H, 连HC ,
则HC
,
则HC
 A
A B
B

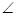 C
C HE为二面角C
HE为二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
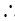 sin
sin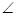 C
C HE=
HE=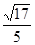
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为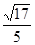 ……… 12分
……… 12分
解法二: (1)分别以直线C B、CC
B、CC 、C
、C A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C
A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, -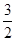 , -
, -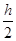 ) ……………………… 3分
) ……………………… 3分

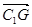 =(2, -
=(2, -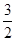 , -
, -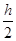 ),
), 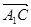 =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分

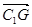 ·
·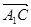 =0,
=0,
 h=3
h=3
(2)设平面A BC
BC 得法向量
得法向量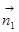 =(a, b, c),则可求得
=(a, b, c),则可求得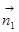 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 点A到平面A
点A到平面A BC
BC 的距离为H=|
的距离为H=|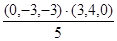 |=
|=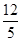 ……… 8分
……… 8分
(3) 设平面A BC的法向量为
BC的法向量为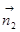 =(x, y, z),则可求得
=(x, y, z),则可求得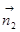 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小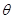 满足cos
满足cos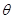 =
=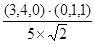 =
=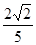 ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为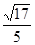
科目:gzsx 来源: 题型:
A.P(x,y,z)中x,y,z的位置可以互换的
B.空间直角坐标系中的点与一个三元有序数组是一种一一对应关系
C.空间直角坐标系中的三条坐标轴把空间分为八个部分
D.某点在不同的空间直角坐标系中的坐标位置可以相同
科目:gzsx 来源:2010-2011年河北冀州中学高一年级下学期期末考试理科数学(B卷) 题型:选择题
在空间直角坐标系中,已知点P(x,y,z),关于下列叙述
①点P关于x轴对称的坐标是P1(x,-y,z)
②点P关于yox轴对称的坐标是P2(x,-y,-z)
③点P关于y轴对称的坐标是P3(x,-y,z)
④点P关于原点对称的坐标是P4(-x,-y,-z),其中正确的个数是 ( )
A.0 B.3 C.2 D.1
科目:gzsx 来源: 题型:
A.P(x,y,z)中x,y,z的位置可以互换的
B.空间直角坐标系中的点与一个三元有序数组是一种一一对应关系
C.空间直角坐标系中的三条坐标轴把空间分为八个部分
D.某点在不同的空间直角坐标系中的坐标位置可以相同
科目:gzsx 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练17练习卷(解析版) 题型:解答题
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为( ,
, ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω:  上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
科目:gzsx 来源:2010-2011年河北冀州中学高一年级下学期期末考试理科数学(B卷) 题型:单选题
在空间直角坐标系中,已知点P(x,y,z),关于下列叙述
①点P关于x轴对称的坐标是P1(x,-y,z)
②点P关于yox轴对称的坐标是P2(x,-y,-z)
③点P关于y轴对称的坐标是P3(x,-y,z)
④点P关于原点对称的坐标是P4(-x,-y,-z),其中正确的个数是 ( )
| A.0 | B.3 | C.2 | D.1 |
科目:gzsx 来源: 题型:
求:(1)线段AB的中点坐标和长度;
(2)到A,B两点距离相等的点P(x,y,z)的坐标x,y,z满足的条件.
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
(1)若x≥0,求动点P(x,![]() )轨迹C的方程;
)轨迹C的方程;
(2)若a=2,不过原点的直线l与x轴,y轴的交点分别为T,S,并且与(1)中轨迹C交于不同的两点P,Q,试求![]() +
+![]() 的取值范围;
的取值范围;
(3)设P(x,y)是平面上的任一点,定义d1(P)=![]()
![]() ,d2(P)=
,d2(P)=![]()
![]() .若在(1)中轨迹C上存在不同的两点A1,A2,使得d1(Ai)=
.若在(1)中轨迹C上存在不同的两点A1,A2,使得d1(Ai)=![]() d2(Ai)(i=1,2)成立,求实数a的取值范围.
d2(Ai)(i=1,2)成立,求实数a的取值范围.
科目:gzsx 来源: 题型:
设函数![]() ,其中,角
,其中,角![]() 的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤
的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤![]() ≤
≤![]()
(1)若点P的坐标为![]() ,求
,求![]() 的值;
的值;
(2)若点P(x,y)为平面区域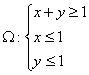 上的一个动点,试确定角
上的一个动点,试确定角![]() 的取值范围,并求函数
的取值范围,并求函数![]() 的最小值和最大值.
的最小值和最大值.
科目:gzsx 来源: 题型:单选题
在空间直角坐标系中,已知点P(x,y,z),关于下列叙述
①点P关于x轴对称的坐标是P1(x,-y,z)
②点P关于yox轴对称的坐标是P2(x,-y,-z)
③点P关于y轴对称的坐标是P3(x,-y,z)
④点P关于原点对称的坐标是P4(-x,-y,-z),
其中正确的个数是
科目:gzsx 来源: 题型:
A.x,y∈R+,![]()
B.x,y,z∈R+,![]()
C.a,b,c∈R+,a+b+c>![]() +
+![]() +
+![]()
D.a,b,c∈R+,(a+b+c)(a2+b2+c2)>9abc