
科目:gzsx 来源: 题型:
[2012·全国卷] 已知正方体ABCD-A1B1C1D1中,E、F分别为BB1、CC1的中点,那么异面直线AE与D1F所成角的余弦值为________.
科目:gzsx 来源: 题型:
2012·全国卷] 已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2![]() ,E为CC1的中点,则直线AC1与平面BED的距离为( )
,E为CC1的中点,则直线AC1与平面BED的距离为( )
A.2 B.![]() C.
C.![]() D.1
D.1
科目:gzsx 来源: 题型:
[2012·全国卷] 如图1-1,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(1)证明:PC⊥平面BED;
(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.

图1-1
科目:gzsx 来源: 题型:
[2012·全国卷] 如图1-1,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(1)证明:PC⊥平面BED;
(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.
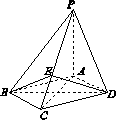
图1-1
科目:gzsx 来源: 题型:
[2012·全国卷] 如图1-1,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2![]() ,PA=2,E是PC上的一点,PE=2EC.
,PA=2,E是PC上的一点,PE=2EC.
(1)证明:PC⊥平面BED;
(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.

图1-1
科目:gzsx 来源: 题型:
(2012·全国高考数学文科试题安徽卷)设集合A={x|-3≤2x-1≤3},集合B是函数y=lg(x-1)的定义域;则A∩B=( )
A.(1,2) B.[1,2]
C.[1,2) D.(1,2]
科目:gzsx 来源: 题型:
[2012·课标全国卷] 如图1-2,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
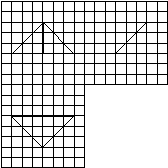
图1-3
A.6 B.9 C.12 D.18
科目:gzsx 来源: 题型:
[2012·课标全国卷] 如图1-4,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC;
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
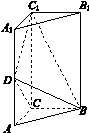
图1-4
科目:gzsx 来源: 题型:
[2012·课标全国卷] 如图1-4,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=![]() AA1,D是棱AA1的中点.
AA1,D是棱AA1的中点.
(1)证明:平面BDC1⊥平面BDC;
(2)平面BDC1分此棱柱为两部分,求这两部分体积的比.
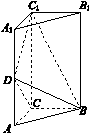
图1-4
科目:gzsx 来源: 题型:
【2012高考真题全国卷理21】(本小题满分12分)(注意:在试卷上作答无效)
已知抛物线C:y=(x+1)2与圆M:(x-1)2+(![]() )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
(Ⅰ)求r;
(Ⅱ)设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离.
科目:gzsx 来源: 题型:
(2012年高考新课标全国卷理科20)(本小题满分12分)
设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() ,已知以
,已知以![]() 为圆心,
为圆心,
![]() 为半径的圆
为半径的圆![]() 交
交![]() 于
于![]() 两点;
两点;
(1)若![]() ,
,![]() 的面积为
的面积为![]() ;求
;求![]() 的值及圆
的值及圆![]() 的方程;
的方程;
(2)若![]() 三点在同一直线
三点在同一直线![]() 上,直线
上,直线![]() 与
与![]() 平行,且
平行,且![]() 与
与![]() 只有一个公共点,
只有一个公共点,
求坐标原点到![]() 距离的比值.
距离的比值.
科目:gzsx 来源: 题型:
(2012年高考全国卷理科21)(本小题满分12分)(注意:在试卷上作答无效)
已知抛物线![]() 与圆
与圆![]() 有一个公共点
有一个公共点![]() ,且在
,且在![]() 处两曲线的切线为同一直线
处两曲线的切线为同一直线![]() 。
。
(1)求![]() ;
;
(2)设![]() 、
、![]() 是异于
是异于![]() 且与
且与![]() 及
及![]() 都相切的两条直线,
都相切的两条直线,![]() 、
、![]() 的交点为
的交点为![]() ,求
,求![]() 到
到![]() 的距离。
的距离。
科目:gzsx 来源: 题型: