科目：gzsx 来源：2010-2011年云南省江高二3月月考数学文卷 题型：解答题
（
请考生在第22~23两题中任选一题做答，如果多做，则按所做的第一题记分。
22．(本小题满分12分)
已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
（1）求f(x)的解析式；
（2）求函数g(x)=f(x2)的单调递增区间.
科目：gzsx 来源：2013-2014学年上海交大附中高三数学理总复习二函数的图像与性质练习卷（解析版） 题型：解答题
已知二次函数f(x)满足条件f(0)＝1，f(x＋1)－f(x)＝2x.
(1)求f(x)；
(2)求f(x)在区间[－1,1]上的最大值和最小值．
科目：gzsx 来源：2012-2013学年河北省高三第一次月考理科数学试卷（解析版） 题型：解答题
(本小题满分12分)已知二次函数f(x)满足条件：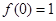
,
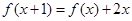
（1）求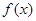
（2）讨论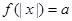 
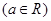的解的个数
科目：gzsx 来源：2010-2011学年河北省石家庄市高三数学练习试卷3 题型：解答题
已知二次函数f(x)满足f (x＋1)－f (x)＝2x且f (0)＝1．
⑴求f (x)的解析式；
⑵在区间[－1，1]上，y＝f (x)的图象恒在y＝2x＋m的图象上方，试确定实数m的范围．
科目：gzsx 来源：2010年延安市高二下学期期末考试（理科）数学卷 题型：解答题
（本小题满分13分）已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式-
⑵求函数g(x)=f(x2)的单调递增区间.
科目：gzsx 来源：2015届山东省济宁市高一下学期期中考试数学试卷（解析版） 题型：解答题
已知二次函数f(x)满足条件f(0)＝1和f(x＋1)－f(x)＝2x.
(1)求f(x)；
(2)求f(x)在区间[－1,1]上的最大值和最小值．
科目：gzsx 来源：0117 期中题 题型：解答题
科目：gzsx 来源：2010-2011年云南省江高二3月月考数学理卷 题型：解答题
.（本小题满分12分）
已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间.
科目：gzsx 来源：2010年湖南省下学期高二单元数学试题 题型：解答题
（本小题满分10分）已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间.
科目：gzsx 来源： 题型：
（1）已知f(
+1)=x+2
,求f(x)，f(x+1),f(x2);
（2）已知二次函数f(x)满足f(0)=1,f(x+1)－f(x)=2x,求f(x);
（3）已知f(x)+
)=2x+1,求f(x).
科目：gzsx 来源： 题型：
已知二次函数f(x)满足：①在x=1时有极值；②图象过点(0,-3)，且在该点处的切线与直线2x+y=0平行．
⑴求f(x)的解析式；
⑵求函数g(x)=f(x2)的单调递增区间.
科目：gzsx 来源： 题型：044
已知二次函数f ( x )满足f ( 2－x ) = f (2 + x )，其图像的顶点为A，图像与x轴交于B(－1，0)和C点，又△ABC的面积为18，求这二次函数的解析式．
科目：gzsx 来源： 题型：044
求函数解析式：?
(1)已知f(
＋1)＝x＋2
，求f(x)，f(x＋1)，f(x2)．?
(2)已知二次函数f(x)满足f(0)＝1，f(x＋1)－f(x)＝2x，求f(x)．?
(3)已知f(x)＋2f(
)＝2x＋1，求f(x)．
科目：gzsx 来源：山东济宁微山一中2011-2012学年高一上学期期中考试数学试题 题型：044
已知二次函数f(x)满足：f(0)＝4，f(2－x)＝f(2＋x)，且该函数的最小值为1．
(1)求此二次函数f(x)的解析式；
(2)若函数f(x)的定义域为A＝[m，n]．(其中0＜m＜n)．问是否存在这样的两个实数m，n，使得函数f(x)的值域也为A？若存在，求出m，n的值；若不存在，请说明理由．
科目：gzsx 来源： 题型：
（12分）已知二次函数f(x)满足f(x-3)=f(-x-3)，且该函数的图像与y轴交于点(0,-1)，在x轴上截得的线段长为
。
确定该二次函数的解析式；
当x∈[-6,-1]时，求f(x)值域。
科目：gzsx 来源：广东省茂名市2012届高三第二次高考模拟考试数学文科试题 题型：044
已知二次函数f(x)满足：①当x＝2时有极值；②图象与y轴交点的纵坐标为－4，且在该点处的切线与直线4x＋y－4＝0平行．
(1)求f(－1)的值；
(2)若m∈R，求函数y＝f(xlnx＋m)，x∈[1，e]的最小值；
(3)若曲线y＝f(lnx)，x∈(1，＋∞)上任意一点处的切线的斜率恒大于k3－k－4，求k的取值范围．
. 
；
的解的个数.
。
＝15，又f(x)＝0的两根立方和等于17，求f(x)的解析式．