科目:gzsx 来源: 题型:
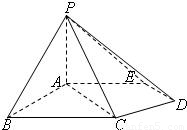
 (2013•杨浦区一模)如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,AP=BC=4,∠ABC=30°,D、E分别是BC、AP的中点,
(2013•杨浦区一模)如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,AP=BC=4,∠ABC=30°,D、E分别是BC、AP的中点,科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
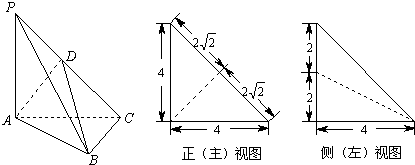
科目:gzsx 来源:2013年上海市杨浦区高考数学一模试卷(文科)(解析版) 题型:解答题

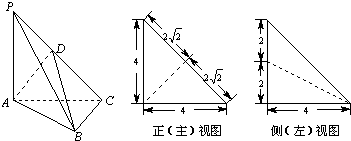
科目:gzsx 来源:2013年上海市杨浦区高考数学一模试卷(理科)(解析版) 题型:解答题
科目:gzsx 来源:2012-2013学年陕西省西安市华清中学高三(下)自主命题数学试卷2(文科)(解析版) 题型:解答题

科目:gzsx 来源: 题型:
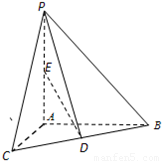
(08年扬州中学) 如图,在四棱锥P―ABC中,PA⊥底面ABCD,∠DAB=90°,AB∥CD,AD=CD=2AB=2,E、F分别为PC、CD的中点
⑴证明:CD⊥平面BEF;
⑵设PA=k・AB,且AD与PC所成的角为60°,求k的值.

科目:gzsx 来源: 题型:
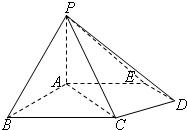 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2| 2 |
科目:gzsx 来源:2011年新疆乌鲁木齐市高二上学期期末考试理科数学卷 题型:解答题
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, 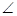 ABC=45°,AB=2
ABC=45°,AB=2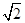 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.

(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积.
科目:gzsx 来源: 题型:
(本小题满分12分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, ![]() ABC=45°,AB=2
ABC=45°,AB=2![]() ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
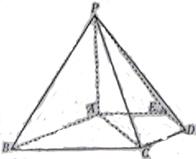 (Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积.
科目:gzsx 来源: 题型:
(本小题满分12分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, ![]() ABC=45°,AB=2
ABC=45°,AB=2![]() ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
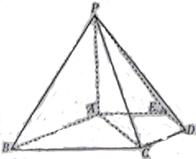 (Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积.
科目:gzsx 来源:2010-2011年四川省成都市玉林中学高二下学期3月月考数学理卷 题型:解答题
(本小题满分14分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=45°,AB=2
ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
(I)求证:平面PCD⊥平面PAC;
(II)求四棱锥P—ACDE的体积.
科目:gzsx 来源:2012-2013学年山东省高三第四次(4月)周测文科数学试卷(解析版) 题型:解答题
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=
ABC= ,AB=2
,AB=2 ,BC=2AE=4,
,BC=2AE=4, 是等腰三角形.
是等腰三角形.

(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求四棱锥P—ACDE的体积.
科目:gzsx 来源:2010-2011年四川省成都市高二下学期3月月考数学理卷 题型:解答题
(本小题满分14分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=45°,AB=2
ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.

(I)求证:平面PCD⊥平面PAC;
(II)求四棱锥P—ACDE的体积.
科目:gzsx 来源: 题型:
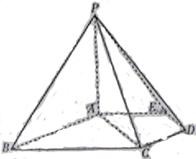
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, ![]() ABC=45°,AB=2
ABC=45°,AB=2![]() ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积.
科目:gzsx 来源:2010年山东省高考数学试卷(理科)(解析版) 题型:解答题
 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.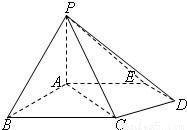
科目:gzsx 来源:2013年天津市耀华中学高考数学一模试卷(文科)(解析版) 题型:解答题
 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
科目:gzsx 来源:2010年高考数学试卷精编:9.3 空间角与距离(解析版) 题型:解答题
 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
科目:gzsx 来源:2010-2011学年湖北省荆州、黄冈、宜昌、襄阳、孝感、十堰、恩施高三(下)4月联考数学试卷B(文科)(解析版) 题型:解答题
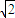 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.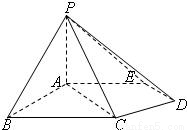
科目:gzsx 来源:2013年高考数学备考复习卷B5:点、直线、平面之间的位置关系(解析版) 题型:解答题
 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.