
科目:gzsx 来源:2010年辽宁省高二下学期第一次月考数学(理) 题型:选择题
如图,在梯形ABCD中,AB//DC,AB=
 。若
。若
 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为 ,则可推算出:
,则可推算出: ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设 ,
, 的面积分别为
的面积分别为 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为 ,则
,则 的面积
的面积 与
与 的关系是( )
的关系是( )
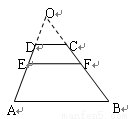
A.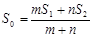 B.
B.
C. D.
D.
科目:gzsx 来源:2010年辽宁省高二下学期第一次月考数学(文) 题型:选择题
如图,在梯形ABCD中,AB//DC,AB=
 。若
。若
 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为 ,则可推算出:
,则可推算出: ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设 ,
, 的面积分别为
的面积分别为 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为 ,则
,则 的面积
的面积 与
与 的关系是( )
的关系是( )

A  B
B

C D
D
科目:gzsx 来源: 题型:

图1-21
科目:gzsx 来源:2010-2011学年湖北省武汉二中、龙泉中学高一下学期期末联考数学 题型:解答题
(12分)在梯形ABCD中AB∥CD,AD=DC=CB= ,
,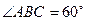 ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE= .
.
(1)求证:BC⊥平面ACFE;
(2)求EC与平面BEF所成角的正弦值.
科目:gzsx 来源:2013届湖北省高一下学期期末联考数学 题型:解答题
(12分)在梯形ABCD中AB∥CD,AD=DC=CB= ,
, ,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=
,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE= .
.
(1)求证:BC⊥平面ACFE;
(2)求EC与平面BEF所成角的正弦值.

科目:gzsx 来源: 题型:
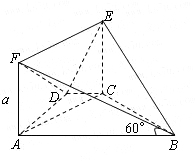
(08年黄冈中学一模文) (12分) 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a , ∠ABC=60°.平面ACEF⊥平面ABCD,且四边形ACEF是矩形,AF=a.
(I)求证:AC⊥BE;
(II)求二面角B-EF-D的余弦值.
科目:gzsx 来源:2012年北师大版高中数学必修5 2.1正余弦定理练习卷(解析版) 题型:解答题
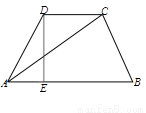
如图所示,已知在梯形ABCD中AB∥CD,CD=2, AC= ,∠BAD=
,∠BAD=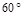 ,求梯形的高.
,求梯形的高.
科目:gzsx 来源: 题型:

(1)求证:BC⊥平面ACFE;
(2)当EM为何值时,AM∥平面BDF?证明你的结论.
科目:gzsx 来源: 题型:

(1)求证:BC⊥平面ACFE;
(2)求二面角B-EF-D所成平面角的余弦值.
科目:gzsx 来源: 题型:

图1-2-7
(1)写出y=f(x)的解析式,并求出函数的定义域;
(2)画出函数的图象并求出函数的值域.
科目:gzsx 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB=2,M,N分别为PA,BC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为正方形,PA=AB=2,M,N分别为PA,BC的中点.科目:gzsx 来源:浙江省期中题 题型:解答题

科目:gzsx 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:047
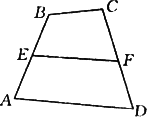
如下图,在四边形ABCD中,已知E、F分别为AB、CD的中点,求证:EF=![]() (AD+BC).
(AD+BC).
科目:gzsx 来源:山东省期末题 题型:解答题

科目:gzsx 来源: 题型:
 已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PA⊥底面ABCD且PA=1,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PA⊥底面ABCD且PA=1,M、N分别为AD、BC的中点,MQ⊥PD于Q.科目:gzsx 来源: 题型:
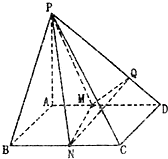 已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.科目:gzsx 来源: 题型:解答题
 已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.科目:gzsx 来源:2011年江西省高考数学仿真押题卷11(文科)(解析版) 题型:解答题

科目:gzsx 来源: 题型:
| AB |
| e1 |
| AD |
| e2 |
| e1 |
| e2 |
| EF |
| BC |
| CD |
| AC |
| EF |
| z1 |
| AC |
| z2 |
| z1 |
| z2 |
| AB |
| BC |
| CD |
| AD |