
科目:gzsx 来源: 题型:
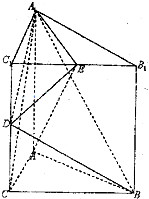 已知三棱柱A1B1C1-ABC中,三个侧面均为矩形,底面ABC为等腰直角三角形,C1C=CA=CB=2,点D为棱CC1的中点,点E在棱B1C1上运动.
已知三棱柱A1B1C1-ABC中,三个侧面均为矩形,底面ABC为等腰直角三角形,C1C=CA=CB=2,点D为棱CC1的中点,点E在棱B1C1上运动.
| ||
| 6 |
| C1E |
| C1B1 |
科目:gzsx 来源:2013年天津市耀华中学高考数学一模试卷(理科)(解析版) 题型:解答题
 ,求
,求 ;
;
科目:gzsx 来源: 题型:
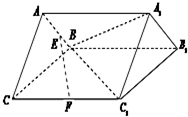 如图,三棱柱ABC-A1B1C1中,BC=2,BC1=
如图,三棱柱ABC-A1B1C1中,BC=2,BC1=| 2 |
| 2 |
| ||
| 3 |
科目:gzsx 来源:2012-2013学年黑龙江省哈尔滨三中高一(下)期末数学试卷(解析版) 题型:解答题
 ,CC1=
,CC1=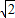 ,△ABC是以BC为底边的等腰三角形,平面ABC⊥平面BCC1B1,E为棱AB的中点,F为CC1上的动点.
,△ABC是以BC为底边的等腰三角形,平面ABC⊥平面BCC1B1,E为棱AB的中点,F为CC1上的动点.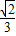 ,求二面角C-AA1-B的余弦值.
,求二面角C-AA1-B的余弦值.
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源:不详 题型:解答题
科目:gzsx 来源:2013年高考数学复习卷D(七)(解析版) 题型:解答题
科目:gzsx 来源:月考题 题型:解答题
科目:gzsx 来源:2008年高考数学模拟创新试题分类汇编(空间几何) 题型:044
已知E为长方体AC1棱AB的中点,AB=2,BC=1,P为棱CC1上的一点(CC1≥1),设PC=x,锐角∠APE的正弦为y

(1)将y表示成关于x的函数;
(2)求出y的最大值,并指出此时点P的位置;
(3)当y取得最大值时,求此时三棱锥P-ABC的体积
科目:gzsx 来源:2014届湖北省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
如图, 三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC, ∠ACB =" 90°," E是棱CC1上动点, F是AB中点, AC =" 1," BC =" 2," AA1 =" 4."

(1) 当E是棱CC1中点时, 求证: CF∥平面AEB1;
(2) 在棱CC1上是否存在点E, 使得二面角A—EB1—B
的余弦值是 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,
请说明理由.
科目:gzsx 来源: 题型:解答题
如图, 三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC, ∠ACB =" 90°," E是棱CC1上动点, F是AB中点, AC =" 1," BC =" 2," AA1 =" 4." 
(1) 当E是棱CC1中点时, 求证: CF∥平面AEB1;
(2) 在棱CC1上是否存在点E, 使得二面角A—EB1—B
的余弦值是 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,
请说明理由.
科目:gzsx 来源: 题型:
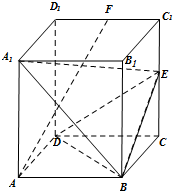 如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,
如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,科目:gzsx 来源: 题型:
 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=1,BC=2,AA1=4.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥底面ABC,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=1,BC=2,AA1=4.2
| ||
| 17 |
科目:gzsx 来源:黑龙江省哈尔滨市第六中学2011届高三第一次模拟考试数学试题(理工类) 题型:044
如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,AA1=3,点E在棱CC1上,点F是棱C1D1的中点

(1)当AF∥平面BDE时,求CE的长;
(2)当CE=1时,求二面角A1―BE―D的余弦值.
科目:gzsx 来源: 题型:解答题
如图,三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC,∠ACB = 90°,E是棱CC1上动点,F是AB中点,AC = 1,BC = 2,AA1 = 4.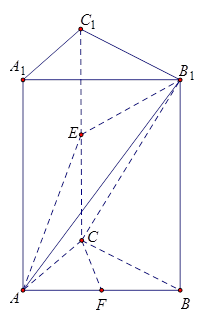
(Ⅰ)当E是棱CC1中点时,求证:CF∥平面AEB1;
(Ⅱ)在棱CC1上是否存在点E,使得二面角A—EB1—B的余弦值是 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.
科目:gzsx 来源:不详 题型:解答题

 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.科目:gzsx 来源: 题型:解答题
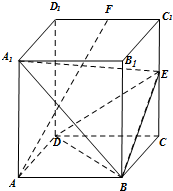 如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,
如图,四棱柱ABCD-A1B1C1D1的底面是边长为2的正方形,AA1⊥底面ABCD,科目:gzsx 来源:2012-2013学年湖北省武汉二中高二(下)期中数学试卷(解析版) 题型:解答题
 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由.
科目:gzsx 来源:2012-2013学年河南省洛阳市偃师高中高三(上)第一次月考数学试卷(解析版) 题型:解答题
