
如图, 三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC, ∠ACB =" 90°," E是棱CC1上动点, F是AB中点, AC =" 1," BC =" 2," AA1 =" 4." 
(1) 当E是棱CC1中点时, 求证: CF∥平面AEB1;
(2) 在棱CC1上是否存在点E, 使得二面角A—EB1—B
的余弦值是 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,
请说明理由.
(1)取AB1的中点G, 联结EG, FG,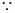 F、G分别是棱AB、AB1中点,
F、G分别是棱AB、AB1中点, 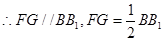
又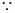 FG∥EC,
FG∥EC, 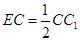 , FG=EC
, FG=EC 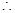 四边形FGEC是平行四边形,
四边形FGEC是平行四边形, 
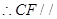 平面AEB.
平面AEB.
(2)在棱CC1上存在点E, 符合题意, 此时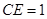
解析试题分析:(1)证明:取AB1的中点G, 联结EG, FG F、G分别是棱AB、AB1中点,
F、G分别是棱AB、AB1中点, 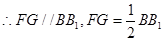
又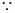 FG∥EC,
FG∥EC, 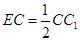 , FG=EC
, FG=EC 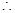 四边形FGEC是平行四边形,
四边形FGEC是平行四边形,  4分
4分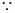 CF
CF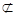 平面AEB1,
平面AEB1, 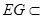 平面AEB1
平面AEB1 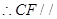 平面AEB. 6分
平面AEB. 6分
(2)解:以C为坐标原点, 射线CA, CB, CC1为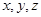 轴正半轴,
轴正半轴,
建立如图所示的空间直角坐标系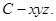
则C(0, 0, 0), A(1, 0, 0), B1(0, 2, 4)
设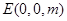
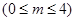 , 平面AEB1的法向量
, 平面AEB1的法向量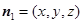 .
.
则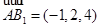 ,
,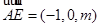
由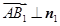 ,
, 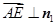
得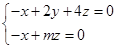
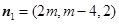 8分
8分 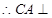 平面
平面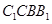
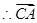 是平面EBB1的法向量,则平面EBB1的法向量
是平面EBB1的法向量,则平面EBB1的法向量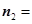
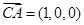 10分
10分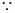 二面角A—EB1—B的平面角余弦值为
二面角A—EB1—B的平面角余弦值为 ,
,
则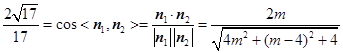 解得
解得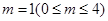
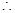 在棱CC1上存在点E, 符合题意, 此时
在棱CC1上存在点E, 符合题意, 此时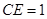 12分
12分
考点:线面平行的判定与二面角的求解
点评:线面平行的判定常借助于面内一直线与面外直线平行来证明,第二问求二面角主要借助了空间直角坐标系将二面角的问题转化为两个半平面的法向量所成角问题


科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,PD⊥平面ABCD,PD=AB=2, E,F,G分别是PC,PD,BC的中点.
(1)求三棱锥E-CGF的体积;
(2)求证:平面PAB//平面EFG;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图甲,在平面四边形ABCD中,已知
 ,
,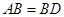 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.

(1)求证:DC 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦值;
(3)求二面角B-EF-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

 是双曲线
是双曲线

 上一点,
上一点, 、
、 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线 ,
,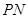 的斜率之积为
的斜率之积为 .
.
(1)求双曲线的离心率;
(2)过双曲线 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于 ,
, 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥E—ABCD中,ABCD是矩形,平面EAB 平面ABCD,AE=EB=BC=2,F为CE上的点,且BF
平面ABCD,AE=EB=BC=2,F为CE上的点,且BF 平面AC E.
平面AC E.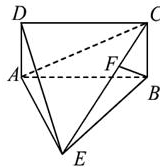
(1)求证:AE BE;
BE;
(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com