
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=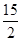 ,求AB的长.
,求AB的长.
科目:高中数学 来源: 题型:解答题
如图所示,四边形ABCD是矩形, ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
(1)求证:AE 平面BCE
平面BCE
(2)求证:AE//平面BFD
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在斜三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,BC=2,BB1=4,AB= ,∠BCC1=60°.
,∠BCC1=60°.
(Ⅰ)求证:C1B⊥平面A1B1C1;
(Ⅱ)求A1B与平面ABC所成角的正切值;
(Ⅲ)若E为CC1中点,求二面角A—EB1—A1的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在正三角形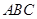 中,
中,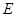 、
、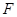 、
、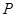 分别是
分别是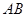 、
、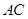 、
、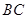 边上的点,满足
边上的点,满足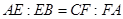
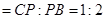 (如图1).将△
(如图1).将△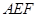 沿
沿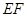 折起到
折起到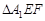 的位置,使二面角
的位置,使二面角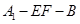 成直二面角,连结
成直二面角,连结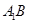 、
、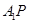 (如图2)
(如图2)
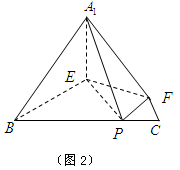
(Ⅰ)求证: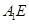 ⊥平面
⊥平面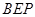 ;
;
(Ⅱ)求二面角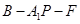 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC— 中,底面
中,底面 为正三角形,
为正三角形,
 平面ABC,
平面ABC, =2AB,N是
=2AB,N是 的中点,M是线段
的中点,M是线段 上的动点。
上的动点。
(1)当M在什么位置时, ,请给出证明;
,请给出证明;
(2)若直线MN与平面ABN所成角的大小为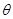 ,求
,求 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图(1),在等腰梯形CDEF中,CB、DA是梯形的高,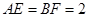 ,
,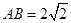 ,现将梯形沿CB、DA折起,使EF//AB且
,现将梯形沿CB、DA折起,使EF//AB且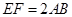 ,得一简单组合体
,得一简单组合体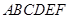 如图(2)所示,已知
如图(2)所示,已知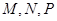 分别为
分别为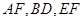 的中点.
的中点.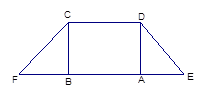
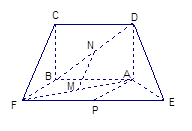
图(1) 图(2)
(Ⅰ)求证: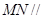 平面
平面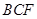 ;
;
(Ⅱ)求证: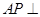 平面
平面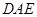 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 三棱柱ABC—A1B1C1的侧棱AA1⊥底面ABC, ∠ACB =" 90°," E是棱CC1上动点, F是AB中点, AC =" 1," BC =" 2," AA1 =" 4." 
(1) 当E是棱CC1中点时, 求证: CF∥平面AEB1;
(2) 在棱CC1上是否存在点E, 使得二面角A—EB1—B
的余弦值是 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,
请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com