
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
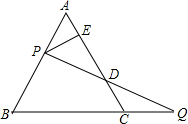 △ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.
△ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.科目:czsx 来源: 题型:解答题
 △ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.
△ABC是边长为2的等边三角形,点P、Q分别从A、C两点同时出发做匀速直线运动,且它们的速度相等.已知点P沿边射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC,垂足是E.科目:czsx 来源: 题型:解答题
 等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P.
等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P.科目:czsx 来源:模拟题 题型:解答题
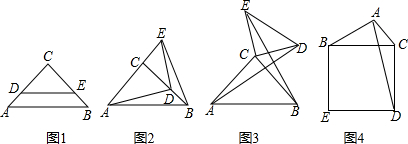
 为直角梯形.动点P从A点出发依次沿线段
为直角梯形.动点P从A点出发依次沿线段 , 向点D移动,设移动路程为x,△
, 向点D移动,设移动路程为x,△ 的面积y关于x的函数关系如图4所示.
的面积y关于x的函数关系如图4所示.  ,请你确定
,请你确定 的长;
的长; ,当点P运动到
,当点P运动到 上,过点P作
上,过点P作 ∥
∥ ,交线段AC于Q(如图2),若线段
,交线段AC于Q(如图2),若线段 的动点N使△
的动点N使△ 为等腰直角三角形,则
为等腰直角三角形,则 的长为多少?
的长为多少? ,当P运动到
,当P运动到 的中点时,连接
的中点时,连接 ,且
,且 与
与 相交于点M,试问以
相交于点M,试问以 为顶点的三角形能否与△
为顶点的三角形能否与△ 相似?若能,请求出图4中a的值;若不能,请说明理由.
相似?若能,请求出图4中a的值;若不能,请说明理由. 
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源:2013年江苏省东台市实验中学中考数学模拟试卷(带解析) 题型:解答题
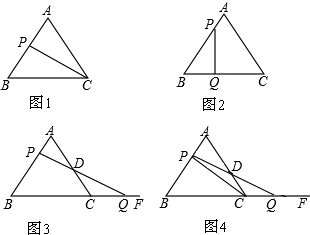
已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.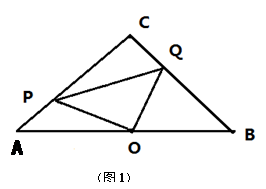
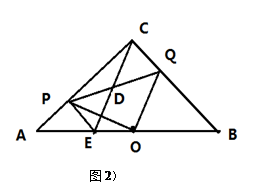
(1)试说明:△POQ是等腰直角三角形;
(2)设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出
S的最大值;
(3)如图2,点P在运动过程中,连结EP、EQ,问四边形PEQC是什么四边形,并说明理由;
(4)求点D运动的路径长(直接写出结果).
科目:czsx 来源:2013年江苏省东台市中考数学模拟试卷(解析版) 题型:解答题
已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.


(1)试说明:△POQ是等腰直角三角形;
(2)设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出
S的最大值;
(3)如图2,点P在运动过程中,连结EP、EQ,问四边形PEQC是什么四边形,并说明理由;
(4)求点D运动的路径长(直接写出结果).
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
已知Rt△ABC,∠ACB=90°,AC=BC=4,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.
(1) 试说明:△POQ是等腰直角三角形;
(2) 设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出
S的最大值;
(3) 如图2,点P在运动过程中,连结EP、EQ,问四边形PEQC是什么四边形,并说明理由;
(4) 求点D运动的路径长(直接写出结果).
 | |||
 | |||
科目:czsx 来源:2012年江苏省泰州市中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源:2012年江苏省扬州市宝应县望直港中学中考数学三模试卷(解析版) 题型:解答题

科目:czsx 来源:不详 题型:解答题


科目:czsx 来源: 题型:
已知R![]() t△A
t△A![]() BC,∠ACB=
BC,∠ACB=![]() 90°,AC=BC=4
90°,AC=BC=4![]() ,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.
,点O是AB中点,点P、Q分别从点A、C出发,沿AC、CB以每秒1个单位的速度运动,到达点C、B后停止。连结PQ、点D是PQ中点,连结CD并延长交AB于点E.
(1) 试说明:△![]() POQ是等腰直角三角形;
POQ是等腰直角三角形;
(2) 设点P、Q运动的时间为t秒,试用含t的代数式来表示△CPQ的面积S,并求出S的最大值;
(3) 如图2,点P在运动过程中,连结EP、EQ,问![]() 四边形PEQC是什么四边形,并说明理由;
四边形PEQC是什么四边形,并说明理由;
(4) 求点D运动的路径长(直接写出结果).

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
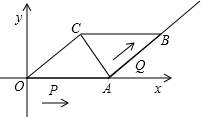 已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.
已知,在平行四边形OABC中,OA=5,AB=4,∠OCA=90°.动点P从0点出发沿射线OA方向以每秒2个单位的速度移动,同时动点Q从A点出发沿射线AB方向以每秒1个单位的速度移动.设移动的时间为t秒.科目:czsx 来源:2015-2016学年山东省八年级上期末数学试卷(解析版) 题型:解答题
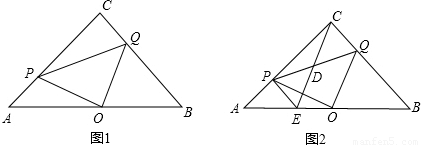
已知,△ABC是边长为4cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度均为1cm/s.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s).

(1)如图1,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
(2)如图2,当t为何值时,△PBQ是直角三角形?
(3)如图3,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,请直接写出∠CMQ度数.
科目:czsx 来源:2017届江苏无锡江阴中学九年级上期中数学试卷(解析版) 题型:解答题
已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.

科目:czsx 来源:2017届江苏无锡江阴市要塞片九年级上期末数学试卷(解析版) 题型:解答题
已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
