矩形ABCD中.AB=4.BC=10.E是AD边中点.矩形沿答案解析
科目:czsx
来源:2011-2012学年福建省永春县八年级上学期期末数学试卷(带解析)
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。

查看答案和解析>>
科目:czsx
来源:2013届福建省永春县八年级上学期期末数学试卷(解析版)
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
② 点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(2)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。

查看答案和解析>>
科目:czsx
来源:
题型:解答题
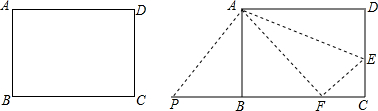
10.【问题情境】
张老师给爱好学习的小军和小俊提出这样的一个问题:如图1,在△ABC中,AB=AC,点P为边BC上任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.

小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
【变式探究】
如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】
图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2$\sqrt{13}$dm,AD=3dm,BD=$\sqrt{37}$dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
10.已知:矩形ABCD中,AB=10,AD=8,点E是BC边上一个动点,将△ABE沿AE折叠得到△AB′E.
(1)如图1,点G和点H分别是AD和AB′的中点,若点B′在边DC上.
①求GH的长;
②求证:△AGH≌△B′CE;
(2)如图2,若点F是AE的中点,连接B′F,B′F∥AD,交DC于I.
①求证:四边形BEB′F是菱形;
②求B′F的长.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
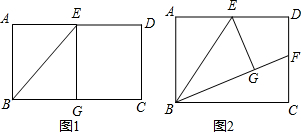
10.如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)如图1,当点G恰好在BC边上时,四边形ABGE的形状是正方形;
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
①求证:BF=AB+DF;
②若AD=$\sqrt{2}$AB,试探索线段DF与FC的数量关系.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.
查看答案和解析>>
科目:czsx
来源:
题型:
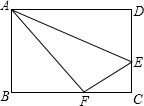
如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=
6
6
,DE=
5
5
.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,矩形ABCD中,AB=8,AD=10,E是CD上一点,把△ADE沿直线AE翻折,D点恰好落在BC边上的F点处,则CE=________.
如图,矩形ABCD中,AB=8,AD=10,E是CD上一点,把△ADE沿直线AE翻折,D点恰好落在BC边上的F点处,则CE=________.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=________,DE=________.
如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=________,DE=________.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,矩形ABCD中,AB=8,AD=10.
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.

查看答案和解析>>
科目:czsx
来源:福建省月考题
题型:填空题
如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=( ),DE=( ).
查看答案和解析>>
科目:czsx
来源:2015-2016学年福建省泉州市泉港区八年级12月质量检测数学试卷(解析版)
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.

(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
② 点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.
查看答案和解析>>
科目:czsx
来源:2015-2016学年福建省泉州市泉港区峰片区八年级上12月月考数学卷(解析版)
题型:解答题
如图,矩形ABCD中,AB=8,AD=10.

(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
②点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,
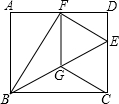
使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
查看答案和解析>>
科目:czsx
来源:
题型:
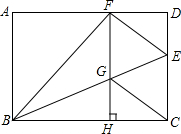
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.
查看答案和解析>>
科目:czsx
来源:2014年初中毕业升学考试(湖南郴州卷)数学(解析版)
题型:填空题
如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点上,则DF的长为 .

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转, 使点E落在BE上的点G处,连接CG.
使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
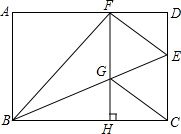 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
(1)求证:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积.
查看答案和解析>>







 如图,矩形ABCD中,AB=8,AD=10.
如图,矩形ABCD中,AB=8,AD=10. 如图,矩形ABCD中,AB=8,AD=10,E是CD上一点,把△ADE沿直线AE翻折,D点恰好落在BC边上的F点处,则CE=________.
如图,矩形ABCD中,AB=8,AD=10,E是CD上一点,把△ADE沿直线AE翻折,D点恰好落在BC边上的F点处,则CE=________. 如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=________,DE=________.
如图,矩形ABCD中,AB=8,AD=10,E是CD上的一点,沿直线AE把△ADE折叠,点D恰好落在边BC上一点F处,则BF=________,DE=________. 如图,矩形ABCD中,AB=8,AD=10.
如图,矩形ABCD中,AB=8,AD=10.



 使点E落在BE上的点G处,连接CG.
使点E落在BE上的点G处,连接CG. 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
 使点E落在BE上的点G处,连接CG.
使点E落在BE上的点G处,连接CG. 如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.
如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,过F作FH⊥BC于H,交BE于G,连接CG.