
科目:gzsx 来源: 题型:
| an |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2k |
| 16 |
| 63 |
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 3 |
科目:czsx 来源: 题型:
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右依次记为A1、A2、A3、…、An,已知第1个正方形中的一个顶点A1的坐标为(1,1),则点A2015的纵坐标为( )
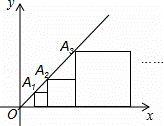
A.2015 B.2014 C.22014 D.22015
科目:czsx 来源: 题型:解答题
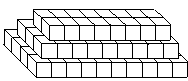
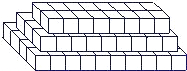
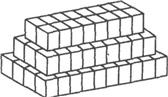
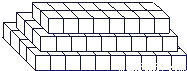
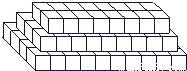
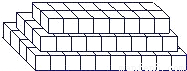
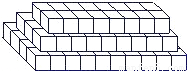
 仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数an与层数n之间满足关系式an=n2-32n+247,1≤n<16,n为整数.
仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数an与层数n之间满足关系式an=n2-32n+247,1≤n<16,n为整数.科目:czsx 来源:浙江省月考题 题型:探究题
仪器箱按如图方式堆放(自下而上依次为第1层、第2层、……),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数an与层数n之间满足关系式an=n2-32n+247,1≤n<16为整数。
(1) 例如,当n=2时,a2=22-32×2+247=187,则a5=_____,a6=_____。
(2)第n层比第(n+1)层多堆放多少个仪器箱?(用含n的代数式表示)。
(3)如果不考虑仪器箱堆放所承受的压力,请根据题设条件判断仪器箱最多可以堆放几层?并说明理由。
(4)设每个仪器箱重54N(牛顿),每个仪器箱能承受的最大压力为160N,并且堆放时每个仪器箱承受的压力是均匀的。
① 若仪器箱仅堆放第1、2两层,求第1层中每个仪器箱承受的平均压力。
② 在确保仪器箱不被损坏的情况下,仪器箱最多可以堆放几层?为什么?
科目:czsx 来源: 题型:
| n(a1+an) |
| 2 |
| 10×(1+28) |
| 2 |
科目:czsx 来源: 题型:
| n(a1+an) |
| 2 |
| 10×(1+28) |
| 2 |
科目:czsx 来源: 题型:解答题
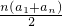 (其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+13+16+19+22+25+28=
(其中n表示数的个数,a1表示第一个数,an表示最后一个数),所以1+4+7+10+13+16+19+22+25+28=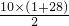 =145.
=145.科目:czsx 来源: 题型:
| n(a1+an) |
| 2 |
| 10×(1+28) |
| 2 |
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
 的压力是均匀的.
的压力是均匀的.科目:czsx 来源: 题型:
 探索、研究:
探索、研究:科目:czsx 来源: 题型:解答题
 的压力是均匀的.
的压力是均匀的.科目:czsx 来源:2009年安徽省马鞍山市二中中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源:2011年安徽省亳州市蒙城县实验中学中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源:2011年辽宁省沈阳市沈河区中考数学一模试卷(解析版) 题型:解答题

科目:czsx 来源: 题型:
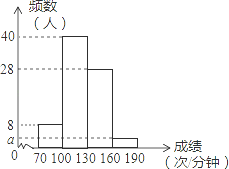
“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
科目:czsx 来源:2007年全国中考数学试题汇编《代数式》(05)(解析版) 题型:解答题
科目:czsx 来源:2007年江苏省镇江市中考数学试卷(解析版) 题型:解答题
科目:czsx 来源:2015年初中毕业升学考试(四川广安卷)数学(解析版) 题型:解答题
(6分)“阳光体育”运动关乎每个学生未来的幸福生活,今年五月,我市某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班选2﹣3名选手参赛,现将80名选手比赛成绩(单位:次/分钟)进行统计.绘制成频数分布直方图,如图所示.
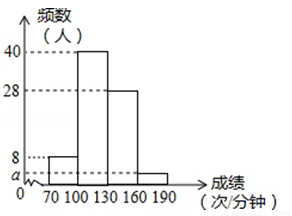
(1)图中a值为 .
(2)将跳绳次数在160~190的选手依次记为A1、A2、…An,从中随机抽取两名选手作经验交流,请用树状或列表法求恰好抽取到的选手A1和A2的概率.
科目:czsx 来源:2015-2016学年江苏省苏州市区七年级上学期期末数学试卷(解析版) 题型:解答题
(2015秋•吴中区期末)在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律的一列数,除了直接相加外,我们还可以用下列公式来求和S, (其中n表示数的个数,a1表示第一个数,an表示最后一个数).所以,1+4+7+10+13+16+19+22+25+28=
(其中n表示数的个数,a1表示第一个数,an表示最后一个数).所以,1+4+7+10+13+16+19+22+25+28= =145.
=145.
用上面的知识解答下面问题:
某公司对外招商承包一个分公司,符合条件的两个企业A、B分别拟定上缴利润方案如下:
A:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元;
B:每半年结算一次上缴利润,第一个半年上缴0.3万元,以年每半年比前半年增加0.3万元.
(1)如果承包期限2年,则A企业上缴利润的总金额为 万元,B企业上缴利润的总金额为 万元;
(2)如果承包期限为n年,则A企业上缴利润的总金额为 万元,B企业上缴利润的总金额为 万元(用含n的代数式表示);
(3)承包期限n=20时,通过计算说明哪个企业上缴利润的总金额比较多?多多少万元?