如图.等边△ABC.D是BC中点.点E,F分别位于AB.AC答案解析
科目:czsx
来源:
题型:
如图,在△ABC中,BC=12,AB=10,sinB=
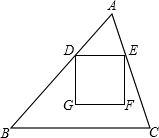
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的
?
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在△ABC中,BC=12,AB=10,sinB=
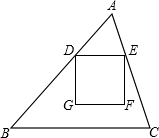
如图,在△ABC中,BC=12,AB=10,sinB= ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的 ?
?
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.
查看答案和解析>>
科目:czsx
来源:2013年重庆市105中学中考数学模拟试卷(解析版)
题型:解答题
如图,在△ABC中,BC=12,AB=10,sinB=

,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的

?
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.

查看答案和解析>>
科目:czsx
来源:2013年河北省邯郸市中考数学押题试卷(解析版)
题型:解答题
如图,在△ABC中,BC=12,AB=10,sinB=

,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的

?
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.

查看答案和解析>>
科目:czsx
来源:2011年河北省保定市中考数学二模试卷(解析版)
题型:解答题
如图,在△ABC中,BC=12,AB=10,sinB=

,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时,EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的

?
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.

查看答案和解析>>
科目:czsx
来源:
题型:
如图1,△ABC中,AB=AC,点O是BC的中点,以O为圆心的⊙O与AB边相切于点D.
(1)判断AC边与⊙O的位置关系,说明理由;
(2)如图2,若AB=5,BC=6,点F为⊙O上一动点,过点F作⊙O的切线分别交AD边、AC边于点G、H,连结OG、OH.
①设∠BAC=α,则∠GOH= (用含α的代数式表示);
②若△OGH是以GH为腰的等腰三角形,求BG的长.


查看答案和解析>>
科目:czsx
来源:2016年初中毕业升学考试(辽宁丹东卷)数学(解析版)
题型:解答题
如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.

(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
查看答案和解析>>
科目:czsx
来源:
题型:
已知△ABC和△EPF都是等腰直角三角形,其中∠ACB=∠EFP=90°,AC=BC,EF=PF.如图1,△ABC的边BC在直线l上,△EPF的边FP也在直线l上,边AC与边EF重合.
(1)在图1中,通过观察、测量,猜想,写出AB与AP所满足的数量关系和位置关系.
答:AB与AP的数量关系和位置关系分别是
、
;
(2)将△EPF沿直线l向左平移到图2的位置时,EP交AC于点Q,连结AP,BQ.请你写出BQ与AP所满足的数量关系和位置关系,并说明理由.
(3)将△EPF 沿直线l向左平移到图3的位置时,EP的延长线交AC 的延长线于点Q,连结AP、BQ.你认
为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
12.如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知等边△ABC中,AB=4.
实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):①以线段AB为直径
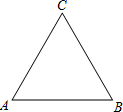
作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.
推理与运用:请根据上述作图解答下面问题:
(1)判断PE与⊙O的位置关系,并说明理由;
(2)若点F是⊙O上一点,且点B是弧EF的中点,则弦EF的长为
.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知等边△ABC中,AB=4.
实践与操作:利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):①以线段AB为直径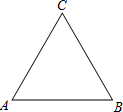 作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.
作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.
推理与运用:请根据上述作图解答下面问题:
(1)判断PE与⊙O的位置关系,并说明理由;
(2)若点F是⊙O上一点,且点B是弧EF的中点,则弦EF的长为______.
查看答案和解析>>
科目:czsx
来源:天津模拟题
题型:解答题
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6。沿斜边AB的中线CD把这张纸片剪成
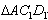
和
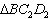
两个三角形(如图2所示)。将纸片
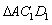
沿直线
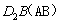
方向平移(点
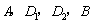
始终在同一直线上),当点
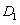
与点B重合时,停止平移。在平移的过程中,

交于点E,
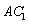
与
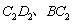
分别交于点F、P。
(1)当
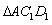
平移到如图3所示位置时,猜想
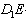
与
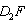
的数量关系,并证明你的猜想;
(2)设平移距离

为x,
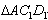
和
重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
(3)对于(2)中的结论是否存在这样的x,使得重复部分面积等于原△ABC纸片面积的
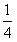
?若存在,请求出x的值;若不存在,请说明理由。
查看答案和解析>>
科目:czsx
来源:
题型:
如图,Rt△ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P,以DE为边向下作等边△DEF,设△DEF与△MBC重叠部分的面积为S(cm2),直线l的运动时间为t( 秒).
秒).
(1)求边BC的长度;
(2)求S与t的函数关系式;
(3)在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
(4)在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2016届江苏省无锡市梁溪区九年级第一次模拟数学试卷(解析版)
题型:解答题
如图,Rt△ABC中,M为斜边AB上一点,且MB=MC=AC=8cm,平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移,运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P,以DE为边向下作等边△DEF,设△DEF与△MBC重叠部分的面积为S(cm2),直线l的运动时间为t(秒).

(1)求边BC的长度;
(2)求S与t的函数关系式;
(3)在整个运动过程中,是否存在这样的时刻t,使得以P、C、F为顶点的三角形为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
(4)在整个运动过程中,是否存在这样的时刻t,使得以点D为圆心、BD为半径的圆与直线EF相切?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
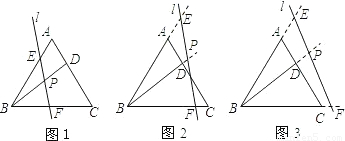
在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60度.
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2,图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),PF=
PE?请写出探
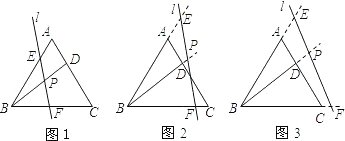
究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
查看答案和解析>>
科目:czsx
来源:
题型:
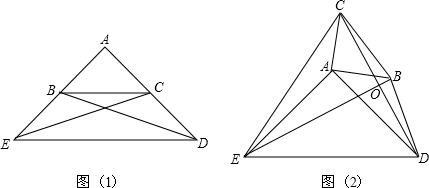
△ADE中,AE=AD且∠AED=∠ADE,∠EAD=90°.
(1)如图(1),若EC、DB分别平分∠AED、∠ADE,交AD、AE于点C、B,连接BC.请你判断AB、AC是否相等,并说明理由;
(2)△ADE的位置保持不变,将(1)中的△ABC绕点A逆时针旋转至图(2)的位置,CD、BE相交于O,请你判断线段BE与CD的位置关系及数量关系,并说明理由;
(3)在(2)的条件下,若CD=6,试求四边形CEDB的面积.
查看答案和解析>>
科目:czsx
来源:2008年泰安市初中毕业升学统一考试、数学试题
题型:044
在等边△ABC中,点D为AC上一点,连结BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60°.
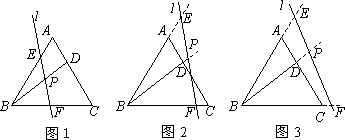
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),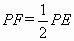 ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60度.
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2,图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),PF= PE?请写出探
PE?请写出探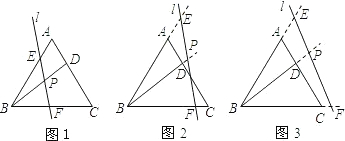 究结果,并说明理由.
究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
查看答案和解析>>
科目:czsx
来源:第25章《图形的变换》中考题集(05):25.1 平移变换(解析版)
题型:解答题
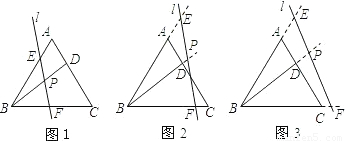
在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60度.
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2,图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),PF=

PE?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
查看答案和解析>>
科目:czsx
来源:第27章《相似》中考题集(30):27.2 相似三角形(解析版)
题型:解答题
在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60度.
(1)如图1,写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图2,图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当BD满足什么条件时(其它条件不变),PF=

PE?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
查看答案和解析>>

 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t, ?
? ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t, ?
?
 ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t, ?
?
 ,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
,动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t, ?
?





 作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.
作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE. 作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.
作圆,圆心为O,AC、BC分别与⊙O交于点D、E;②延长AB到点P,使BP=OB,连接PE.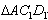 和
和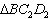 两个三角形(如图2所示)。将纸片
两个三角形(如图2所示)。将纸片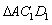 沿直线
沿直线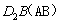 方向平移(点
方向平移(点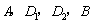 始终在同一直线上),当点
始终在同一直线上),当点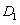 与点B重合时,停止平移。在平移的过程中,
与点B重合时,停止平移。在平移的过程中, 交于点E,
交于点E,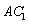 与
与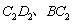 分别交于点F、P。
分别交于点F、P。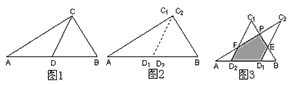
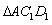 平移到如图3所示位置时,猜想
平移到如图3所示位置时,猜想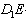 与
与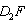 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想; 为x,
为x,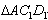 和
和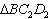 重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;
重复部分面积为y,请写出y与x的函数关系式,以及自变量的取值范围;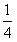 ?若存在,请求出x的值;若不存在,请说明理由。
?若存在,请求出x的值;若不存在,请说明理由。  秒).
秒).

 究结果,并说明理由.
究结果,并说明理由.
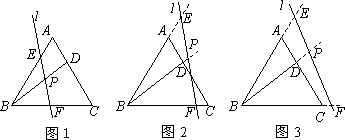
![]() ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由. PE?请写出探
PE?请写出探 究结果,并说明理由.
究结果,并说明理由. PE?请写出探究结果,并说明理由.
PE?请写出探究结果,并说明理由.
 PE?请写出探究结果,并说明理由.
PE?请写出探究结果,并说明理由.