
科目:czsx 来源: 题型:
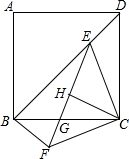 如图,正方形ABCD中,E为对角线BD上一点,且BE=BC,连接CE,将△CDE绕点C逆时针旋转90°,得到△CBF.连接EF,交BC于点G,H为EF的中点,连接CH,则下列说法:①△CDE≌△EBG;②BC平分∠HCF;③S△BGF=S△CGF;④FG=GH;⑤在不添加其他线段的条件下,图中有8个等腰三角形,其中正确的说法是( )
如图,正方形ABCD中,E为对角线BD上一点,且BE=BC,连接CE,将△CDE绕点C逆时针旋转90°,得到△CBF.连接EF,交BC于点G,H为EF的中点,连接CH,则下列说法:①△CDE≌△EBG;②BC平分∠HCF;③S△BGF=S△CGF;④FG=GH;⑤在不添加其他线段的条件下,图中有8个等腰三角形,其中正确的说法是( )科目:czsx 来源: 题型:单选题
 如图,正方形ABCD中,E为对角线BD上一点,且BE=BC,连接CE,将△CDE绕点C逆时针旋转90°,得到△CBF.连接EF,交BC于点G,H为EF的中点,连接CH,则下列说法:①△CDE≌△EBG;②BC平分∠HCF;③S△BGF=S△CGF;④FG=GH;⑤在不添加其他线段的条件下,图中有8个等腰三角形,其中正确的说法是
如图,正方形ABCD中,E为对角线BD上一点,且BE=BC,连接CE,将△CDE绕点C逆时针旋转90°,得到△CBF.连接EF,交BC于点G,H为EF的中点,连接CH,则下列说法:①△CDE≌△EBG;②BC平分∠HCF;③S△BGF=S△CGF;④FG=GH;⑤在不添加其他线段的条件下,图中有8个等腰三角形,其中正确的说法是科目:czsx 来源: 题型:
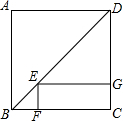 如图,正方形ABCD中,E是对角线BD上一点,过E点作矩形EFCG,其中点F在BC上,点G在DC上.
如图,正方形ABCD中,E是对角线BD上一点,过E点作矩形EFCG,其中点F在BC上,点G在DC上.科目:czsx 来源: 题型:填空题
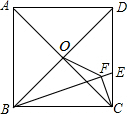 如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.
如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$. 科目:czsx 来源: 题型:
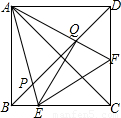
 已知:如图,正方形ABCD中,AC,BD为对角线,将∠BAC绕顶点A逆时针旋转α°(0<α<45),旋转后角的两边分别交BD于点P、点Q,交BC,CD于点E、点F,连接EF,EQ.
已知:如图,正方形ABCD中,AC,BD为对角线,将∠BAC绕顶点A逆时针旋转α°(0<α<45),旋转后角的两边分别交BD于点P、点Q,交BC,CD于点E、点F,连接EF,EQ.科目:czsx 来源:北京市石景山区2011年初中毕业暨中考一模数学试题 题型:044
已知:如图,正方形ABCD中,AC,BD为对角线,将∠BAC绕顶点A逆时针旋转α°(0<α<45),旋转后角的两边分别交BD于点P、点Q,交BC,CD于点E、点F,联结EF,EQ.
(1)在∠BAC的旋转过程中,∠AEQ的大小是否改变,若不变写出它的度数,若改变,写出它的变化范围(直接在答题卡上写出结果,不必证明);
(2)探究△APQ与△AEF的面积的数量关系,写出结论并加以证明.

科目:czsx 来源: 题型:解答题
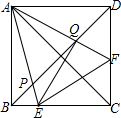 已知:如图,正方形ABCD中,AC,BD为对角线,将∠BAC绕顶点A逆时针旋转α°(0<α<45),旋转后角的两边分别交BD于点P、点Q,交BC,CD于点E、点F,连接EF,EQ.
已知:如图,正方形ABCD中,AC,BD为对角线,将∠BAC绕顶点A逆时针旋转α°(0<α<45),旋转后角的两边分别交BD于点P、点Q,交BC,CD于点E、点F,连接EF,EQ.科目:czsx 来源:2013年北京市人大附中中考数学冲刺试卷(一)(解析版) 题型:解答题

科目:czsx 来源:2011年北京市石景山区中考数学一模试卷(解析版) 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源:2014-2015学年四川省阶段教育学校招生适应性考试数学试卷(解析版) 题型:解答题
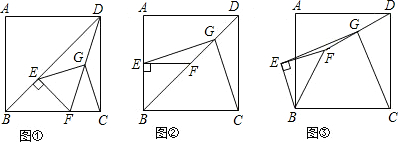
(本小题满分11分)已知正方形ABCD,E为对角线BD上一点,过E点作EF丄BD交BC于F,连接DF,G为DF中点,连接EG,CG.
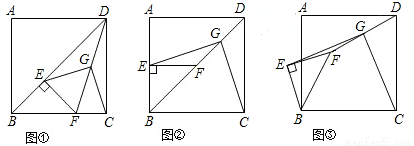
(1)求证:EG=CG;
(2)将图①中的△BEF绕B点逆时针旋转45°,如图②,取DF的中点G,连接EG,CG.你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明.
(3)将图①中的△BEF绕B点旋转任意角度,如图③,再连接相应的线段,则(1)中的结论是否仍然成立?(不要求证明)
科目:czsx 来源: 题型:
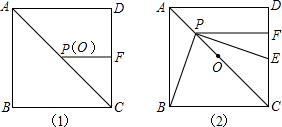 在正方形ABCD中,O是对角线AC的中点,P是对角线AC上的一动点,过点P作PF⊥CD于点F,如图(1),当点P与点O重合时,显然有DF=CF.如图(2),若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E,
在正方形ABCD中,O是对角线AC的中点,P是对角线AC上的一动点,过点P作PF⊥CD于点F,如图(1),当点P与点O重合时,显然有DF=CF.如图(2),若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E,| 2 |
科目:czsx 来源: 题型:解答题
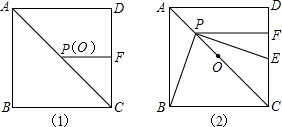 在正方形ABCD中,O是对角线AC的中点,P是对角线AC上的一动点,过点P作PF⊥CD于点F,如图(1),当点P与点O重合时,显然有DF=CF.如图(2),若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E,
在正方形ABCD中,O是对角线AC的中点,P是对角线AC上的一动点,过点P作PF⊥CD于点F,如图(1),当点P与点O重合时,显然有DF=CF.如图(2),若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E,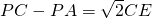 .
.科目:czsx 来源:期末题 题型:证明题

 。
。科目:czsx 来源:2011-2012学年湘教版九年级(上)期末数学试卷(一)(解析版) 题型:解答题
 .
.
科目:czsx 来源:2009-2010学年贵州省铜仁市九年级(上)期末数学试卷(解析版) 题型:解答题
 .
.
科目:czsx 来源: 题型:
| S1 | S2 |
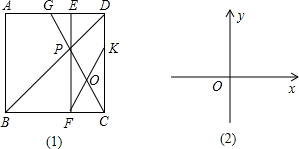 面的直角坐标系中画出这个函数的图象.
面的直角坐标系中画出这个函数的图象. 科目:czsx 来源:2008年北京市门头沟区初三二模数学试题 题型:044
如图,正方形ABCD绕点A逆时针旋转n°后得到正方形AEFG,边EF与CD交于点O.
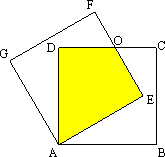
(1)请在图中连结两条线段(正方形的对角线除外).要求:①所连结的两条线段是以图中已标有字母的点为端点;②所连结的两条线段互相垂直.
(2)若正方形的边长为2 cm,重叠部分(四边形AEOD)的面积为![]() ,旋转的角度n是多少度?请说明理由.
,旋转的角度n是多少度?请说明理由.
科目:czsx 来源: 题型:解答题
 .求y关于x的函数关系式及自变量x的取值范围,并在下
.求y关于x的函数关系式及自变量x的取值范围,并在下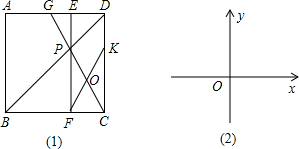 面的直角坐标系中画出这个函数的图象.
面的直角坐标系中画出这个函数的图象.