
科目:czsx 来源: 题型:
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y= x的图象的交点
x的图象的交点 为C(m,4).
为C(m,4).

(1)求一次函数y=kx+b的解析式.
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,求点D的坐标.
科目:czsx 来源: 题型:
如图,在平面直角坐标系xOy中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() (-1,0)、
(-1,0)、![]() (3,0)两点, 顶点为
(3,0)两点, 顶点为![]() .
.
(1) 求此二次函数解析式;![]()
(2) 点![]() 为点
为点![]() 关于x轴的对称点,过点
关于x轴的对称点,过点![]() 作直线
作直线![]() :
:![]() 交BD于点
交BD于点![]() E,过点
E,过点![]() 作直线
作直线![]() ∥
∥![]() 交直线
交直线![]() 于
于![]() 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若![]() 、
、![]() 分
分![]() 别为直线
别为直线![]() 和直线
和直线![]() 上的两个动点,连结
上的两个动点,连结![]() 、
、![]() 、
、![]() ,求
,求![]() 和的最小值.
和的最小值.
科目:czsx 来源:2013届北京市龙文教育九年级第一次中考模拟数学试卷(带解析) 题型:解答题
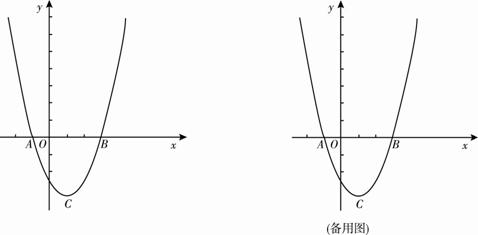
如图,在平面直角坐标系xOy中,二次函数 的图象与
的图象与 轴交于
轴交于 (-1,0)、
(-1,0)、 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.
(1) 求此二次函数解析式;
(2) 点 为点
为点 关于x轴的对称点,过点
关于x轴的对称点,过点 作直线
作直线 :
: 交BD于点E,过点
交BD于点E,过点 作直线
作直线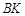 ∥
∥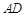 交直线
交直线 于
于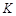 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若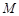 、
、 分别为直线
分别为直线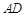 和直线
和直线 上的两个动点,连结
上的两个动点,连结 、
、 、
、 ,求
,求 和的最小值.
和的最小值.
科目:czsx 来源:2012-2013学年北京市龙文教育九年级第一次中考模拟数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,二次函数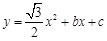 的图象与
的图象与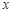 轴交于
轴交于 (-1,0)、
(-1,0)、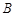 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.

(1) 求此二次函数解析式;
(2) 点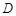 为点
为点 关于x轴的对称点,过点
关于x轴的对称点,过点 作直线
作直线 :
: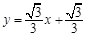 交BD于点E,过点
交BD于点E,过点 作直线
作直线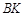 ∥
∥ 交直线
交直线 于
于 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,若 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连结
上的两个动点,连结 、
、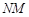 、
、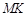 ,求
,求 和的最小值.
和的最小值.
科目:czsx 来源:不详 题型:解答题
 的图象与
的图象与 轴交于
轴交于 (-1,0)、
(-1,0)、 (3,0)两点, 顶点为
(3,0)两点, 顶点为 .
.
 为点
为点 关于x轴的对称点,过点
关于x轴的对称点,过点 作直线
作直线 :
: 交BD于点E,过点
交BD于点E,过点 作直线
作直线 ∥
∥ 交直线
交直线 于
于 点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由;
点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等,若存在,请求出点P的坐标;若不存在,请说明理由; 、
、 分别为直线
分别为直线 和直线
和直线 上的两个动点,连结
上的两个动点,连结 、
、 、
、 ,求
,求 和的最小值.
和的最小值.科目:czsx 来源:2013-2014学年内蒙古鄂尔多斯市毕业升学第二次模拟考试数学试卷(解析版) 题型:解答题
如图在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=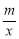 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE= .
.
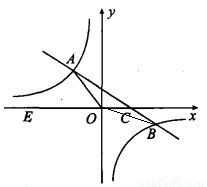
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式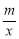 ﹤kx+b的x的取值范围.
﹤kx+b的x的取值范围.
科目:czsx 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
在平面直角坐标系xOy中,已知直线y=-![]() x+
x+![]() 交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图①所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图①所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的![]() 处,如图②所示.
处,如图②所示.


(1)求图①中的点B的坐标;
(2)求α的值;
(3)若二次函数y=mx2+3x的图象经过(1)中的点B,判断点![]() 是否在这条抛物线上,并说明理由.
是否在这条抛物线上,并说明理由.
科目:czsx 来源: 题型:解答题
 x+
x+ 交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.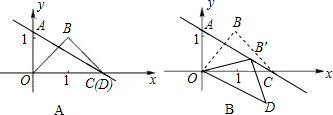
科目:czsx 来源:2013年3月中考数学模拟试卷(3)(解析版) 题型:解答题
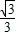 x+
x+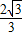 交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.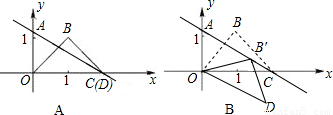
科目:czsx 来源:2007年北京市海淀区中考数学二模试卷(解析版) 题型:解答题
 x+
x+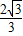 交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.
交x轴于点C,交y轴于点A.等腰直角三角板OBD的顶点D与点C重合,如图A所示.把三角板绕着点O顺时针旋转,旋转角度为α(0°<α<180°),使B点恰好落在AC上的B'处,如图B所示.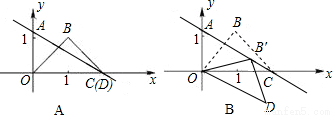
科目:czsx 来源:不详 题型:解答题
| ||
| 3 |
2
| ||
| 3 |

科目:czsx 来源: 题型:
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
科目:czsx 来源: 题型:
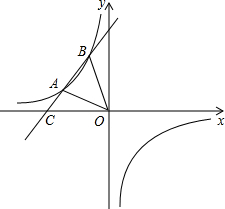 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函y=| m |
| x |
| 3 |
| 4 |
| m |
| x |
科目:czsx 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数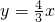 的图象的交点为C(m,4).
的图象的交点为C(m,4).科目:czsx 来源: 题型:解答题
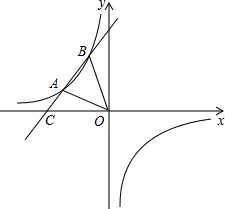 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函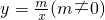 的图象交于第二象限内的A、B两点,与x轴交于点C.已知OA=5,tan∠AOC=
的图象交于第二象限内的A、B两点,与x轴交于点C.已知OA=5,tan∠AOC= ,点B的纵坐标为6.
,点B的纵坐标为6.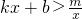 的解集.
的解集.科目:czsx 来源:2013年重庆市西南大学附属中学中考数学二模试卷(解析版) 题型:解答题
 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函 的图象交于第二象限内的A、B两点,与x轴交于点C.已知OA=5,tan∠AOC=
的图象交于第二象限内的A、B两点,与x轴交于点C.已知OA=5,tan∠AOC= ,点B的纵坐标为6.
,点B的纵坐标为6.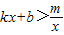 的解集.
的解集.科目:czsx 来源:2013年北京市龙文教育中考数学一模试卷(解析版) 题型:解答题
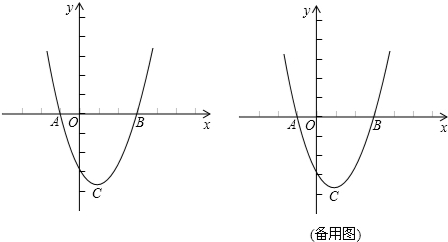
 的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为C.
的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为C.
 交BD于点E,过点B作直线BK∥AD交直线l于K点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等?若存在,请求出点P的坐标;若不存在,请说明理由;
交BD于点E,过点B作直线BK∥AD交直线l于K点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等?若存在,请求出点P的坐标;若不存在,请说明理由;科目:czsx 来源:2014-2015学年江苏省盐城市盐都区西片八年级12月月考数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y= 的图象交点为C(m,4)求:
的图象交点为C(m,4)求:

(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标。
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
科目:czsx 来源: 题型:
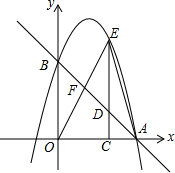 如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴相交于点A(4,0),与y轴相交于点B(0,4),动点C是从点A出发,向O点运动,到达0点时停止运动,过点C作EC⊥x轴,交直线AB于点D,交抛物线于点E.科目:czsx 来源: 题型:
 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=| 4 |
| 3 |