如图13.抛物线y+αX2+bX+c与X轴交于A.与Y轴交于点C(0,2).答案解析
科目:czsx
来源:
题型:解答题
13.

如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.如图,抛物线y=-x
2+bx+c与直线y=$\frac{1}{2}$x+2交于C,D两点,其中点 C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
(1)求抛物线的解析式;
(2)若点P在直线BC上部的抛物线上运动,是否存在这样的点P,使得△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图,已知c>0,抛物线y=-x
2+bx+c与x轴交于A(x
1,0),B(x
2,0)两点(x
2>x
1),与y轴交于点C.
(1)若x
2=1,BC=$\sqrt{5}$,求函数y=x
2+bx+c的最小值;
(2)若$\frac{OC}{OA}$=2,求抛物线y=-x
2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
6.

如图,抛物线y=$\frac{1}{2}$x
2+bx+c与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C点D在函数图象上.
(1)求该抛物线的函数关系式;
(2)设点D的横坐标为m(-4<m<0),四边形ADCB的面积为S,求S与m之间的函数关系式,并写出S的取值范围;
(3)当(2)中的S=13时,求点D的横坐标;
(4)若点E是线段BC的中点,点P是抛物线对称轴上的一点,设点P的纵坐标为t,请直接写出当△PEB为钝角三角形时t的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.
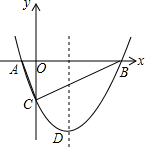
如图,抛物线y=$\frac{1}{2}$x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)抛物线上是否存在一点P,试的△BCD面积与△PBC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.在平面直角坐标系中,已知抛物线y=x
2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
(1)填空:b=2,c=-3,直线AC的解析式为y=-x-3;
(2)直线x=t与x轴相交于点H.
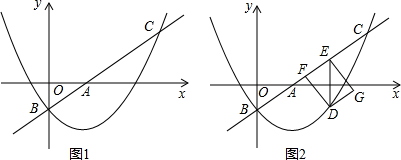
①当t=-3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当-3<t<-1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为$\frac{3}{5}$,求此时t的值.
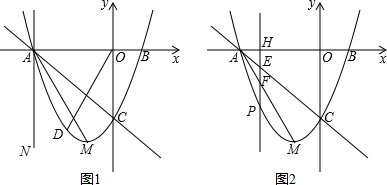
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.如图1,已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,抛物线y=-x
2+bx+c过A、B两点,且与x轴交于另一点C.
(1)求b、c的值;
(2)如图1,点D为AC的中点,点E在线段BD上,且BE=2ED,连接CE并延长交抛物线于点M,求点M的坐标;
(3)将直线AB绕点A按逆时针方向旋转15°后交y轴于点G,连接CG,如图2,P为△ACG内一点,连接PA、PC、PG,分别以AP、AG为边,在他们的左侧作等边△APR,等边△AGQ,连接QR
①求证:PG=RQ;
②求PA+PC+PG的最小值,并求出当PA+PC+PG取得最小值时点P的坐标.
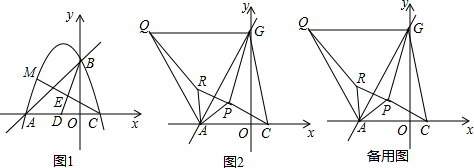
查看答案和解析>>
科目:czsx
来源:
题型:
如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=-
x
2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,点F在直线AD上且横坐标为6.
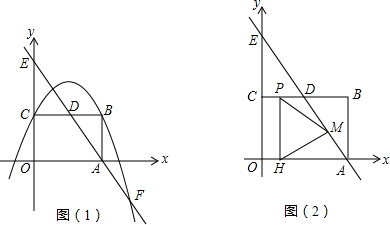
(1)求该抛物线解析式并判断F点是否在该抛物线上;
(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;
同时,动点M从点A出发,沿线段AE以每秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,求出此时t的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.

(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线
l′∥
l,交抛物线于点
N,连接
CN、
BN,设点
M的横坐标为
t.当
t为何值时,△
BCN的面积最大?最大面积为多少?
查看答案和解析>>
科目:czsx
来源:2010年高级中等学校招生全国统一考试数学卷(云南红河)
题型:解答题
如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.

(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=
-x
2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
-x
2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.如图1,直线l:y=$\frac{3}{4}$x+m与x轴、y轴分别交于点A和点B(0,-1),抛物线y=$\frac{1}{2}$x
2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A
1O
1B
1,点A、O、B的对应点分别是点A
1、O
1、B
1.若△A
1O
1B
1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A
1的横坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
(2013•金华模拟)如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=
-x
2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=
-x
2+bx+c交于第四象限的F点.
(1)求该抛物线解析式与F点坐标;
(2)如图(2),动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE以每秒
个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.
①问EP+PH+HF是否有最小值?如果有,求出t的值;如果没有,请说明理由.
②若△PMH是等腰三角形,请直接写出此时t的值.

查看答案和解析>>
科目:czsx
来源:
题型:
(2010四川乐山)如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?O4YR%I2UNRAMG.jpg)

查看答案和解析>>
科目:czsx
来源:
题型:
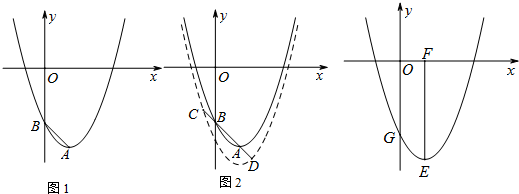
如图1,抛物线C
1:y=x
2+bx+c的顶点为A
(1,-),与y轴的负半轴交于B点.
(1)求抛物线C
1的解析式及B点的坐标;
(2)如图2,将抛物线C
1向下平移与直线AB相交于C、D两点,若BC+AD=AB,求平移后的抛物线C
2的解析式;
(3)如图3在(2)中,设抛物线C
2与y轴交于G点,顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNG=90°,请你分析实数m的变化范围.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图,已知抛物线y=-x
2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式;
(2)点M在直线x=3上,求使MN+MD的值最小时的M点坐标;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
(2012•郴州)阅读下列材料:
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+By+C=0的距离(d)计算公式是:d=
.

例:求点P(1,2)到直线y=
x-
的距离d时,先将y=
x-化为5x-12y-2=0,再由上述距离公式求得d=
=
.
解答下列问题:
如图2,已知直线y=-
x-4与x轴交于点A,与y轴交于点B,抛物线y=x
2-4x+5上的一点M(3,2).
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>

 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
 如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C. 如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C点D在函数图象上.
如图,抛物线y=$\frac{1}{2}$x2+bx+c与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C点D在函数图象上. 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).







O4YR%I2UNRAMG.jpg)


 如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
如图,已知抛物线y=-x2+bx+c与一直线相交于A(-1,0),C(2,3)两点,与y轴交于点N.其顶点为D.