科目：gzsx 来源： 题型：

设m＜0，角α的终边经过点P（-3m，4m），那么sinα+2cosα的值等于

2

5

2

5

．

查看答案和解析>>

科目：gzsx 来源： 题型：解答题

设函数f（x）=ax²+bx+c（a，b，c为实数，且a≠0），F（x）= $数学公式$
（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求f（x）的表达式；
（2）在（Ⅰ）在条件下，当x∈[-1，1]时，g（x）=kx-f（x）是单调函数，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．

查看答案和解析>>

科目：gzsx 来源：2009-2010学年湖南省长沙市同升湖实验学校高三（上）第三次月考数学试卷（文科）（解析版） 题型：解答题

设函数f（x）=ax²+bx+c（a，b，c为实数，且a≠0），

（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求F（x）的表达式；
（2）在（Ⅰ）在条件下，当时，，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．

查看答案和解析>>

科目：gzsx 来源：2012-2013学年广东省揭阳市普宁市城东中学高三（上）第三次月考数学试卷（文科）（解析版） 题型：解答题

设函数f（x）=ax²+bx+c（a，b，c为实数，且a≠0），F（x）=

（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求f（x）的表达式；
（2）在（Ⅰ）在条件下，当x∈[-1，1]时，g（x）=kx-f（x）是单调函数，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．

查看答案和解析>>

科目：gzsx 来源：2009-2010学年北京市东城区高三（上）期末教学试卷（文科）（解析版） 题型：解答题

设函数f（x）=ax²+bx+c（a，b，c为实数，且a≠0），

（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求F（x）的表达式；
（2）在（Ⅰ）在条件下，当时，，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．

查看答案和解析>>

科目：gzsx 来源：2010年高考考试策略专题训练（一）（解析版） 题型：解答题

设函数f（x）=ax²+bx+c（a，b，c为实数，且a≠0），

（1）若f（-1）=0，曲线y=f（x）通过点（0，2a+3），且在点（-1，f（-1））处的切线垂直于y轴，求F（x）的表达式；
（2）在（Ⅰ）在条件下，当时，，求实数k的取值范围；
（3）设mn＜0，m+n＞0，a＞0，且f（x）为偶函数，证明F（m）+F（n）＞0．

查看答案和解析>>

科目：gzsx 来源： 题型：填空题

设m＜0，角α的终边经过点P（-3m，4m），那么sinα+2cosα的值等于________．

查看答案和解析>>

科目：gzsx 来源：不详 题型：填空题

设m＜0，角α的终边经过点P（-3m，4m），那么sinα+2cosα的值等于______．

查看答案和解析>>

科目：gzsx 来源：2008-2009学年重庆市南开中学高三总复习数学试卷（2）（解析版） 题型：解答题

设m＜0，角α的终边经过点P（-3m，4m），那么sinα+2cosα的值等于．

查看答案和解析>>

科目：gzsx 来源： 题型：

设m＜0，点M（3m，-m）为角α的终边上一点，则

1

2sinαcosα+cos2α

的值为（　　）

A、

10

7

B、-2

C、

2

3

D、

10

3

查看答案和解析>>

科目：gzsx 来源： 题型：

设m＜0，角α的终边经过点P（4m，-3m），那么2sinα+cosα的值等于（　　）

A、

2

5

B、-

2

5

C、

1

5

D、-

1

5

查看答案和解析>>

科目：gzsx 来源： 题型：选择题

4．设m＜0，点M（m，-2m）为角α的终边上一点，则$\frac{1}{{2sinαcosα+{{cos}^2}α}}$的值为（　　）

A．

$-\frac{5}{3}$

B．

-2

C．

$\frac{2}{3}$

D．

$\frac{10}{3}$

查看答案和解析>>

科目：gzsx 来源： 题型：

设点P（x₀，y₀）在直线x=m（y≠±m，0＜m＜1）上，过点P作双曲线x²-y²=1的两条切线PA、PB，切点为A、B，定点M(

1

m

，0)．
（1）求证：三点A、M、B共线．
（2）过点A作直线x-y=0的垂线，垂足为N，试求△AMN的重心G所在曲线方程．

查看答案和解析>>

科目：gzsx 来源： 题型：

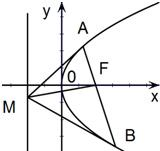设抛物线y²=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x₁，y₁）、（x₂，y₂），y₁＞0，y₂＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：K_MA=a，K_MF=b，K_MB=c，（如图）
（I）若y₁y₂=-4，求抛物线的方程；
（II）当b=2时，求a+c的值；
（III）如果取KMA=2，KMB=-

1

2

时，判定|∠AMF-∠BMF|和∠MFO的值大小关系．并说明理由．

查看答案和解析>>

科目：gzsx 来源： 题型：

设抛物线y²=4px（p＞0）的准线与x轴的交点为M，过点M作直线l交抛物线于A，B两点．若直线l的斜率依次取p，p²，…，pⁿ时，线段AB的垂直平分线与对称轴的交点依次为N₁，N₂，…，N_n，当0＜p＜1时，求S=

1

|N1N2|

+

1

|N2N3|

+…+

1

NnNn+1

+…的值．

查看答案和解析>>

科目：gzsx 来源： 题型：

设函数f（x）=x³-

1

2

x²-2x+m，若f（x）在[0，2]上没有零点，则实数m的取值范围为

m＜-2或m＞

3

2

m＜-2或m＞

3

2

．

查看答案和解析>>

科目：gzsx 来源： 题型：

设f（log_ax）=

a(x2-1)

x(a2-1)

（1）求f（x）的表达式，并判断f（x）的奇偶性；
（2）试证明：函数f（x）的图象上任意两点的连线的斜率大于0；
（3）对于f（x），当x∈（-1，1）时，恒有f（1-m）+f（1-m²）＜0求m的取值范围．

查看答案和解析>>

科目：gzsx 来源： 题型：

设函数f（x）=-x（x-m）²．
（Ⅰ）当m=1时，求曲线y=f（x）在点（2，f（2））处的切线的方程；
（Ⅱ）当m＜0时，求函数f（x）的单调增区间和极小值．

查看答案和解析>>

科目：gzsx 来源： 题型：

设抛物线y²=4px（p＞0）的准线与x轴的交点为M，过点M作直线l交抛物线于A，B两点．
（1）求线段AB中点的轨迹方程；
（2）若线段AB的垂直平分线交x轴于N（x₀，0），求证：x₀＞3p；
（3）若直线l的斜率依次取p，p²，…，pⁿ时，线段AB的垂直平分线与x轴的交点依次为N₁，N₂，…，N_n，当时0＜p＜1，求Sn-1=

1

|N1N2|

+

1

|N2N3|

+…+

1

|Nn-1Nn|

(n≥2，n∈N*)的值．

查看答案和解析>>

科目：gzsx 来源：江西省德兴一中2011－2012学年高二下学期第一次月考数学文科试题 题型：044

设函数f(x)＝－x³＋x²＋(m²－1)x，(x∈R，)其中m＞0

(Ⅰ)当m＝1时，曲线y＝f(x)在点(1，f(1))处的切线斜率

(Ⅱ)求函数的单调区间与极值；

(Ⅲ)已知函数f(x)有三个互不相同的零点0，x₁，x₂，且x₁＜x₂．若对任意的x∈[x₁，x₂]，f(x)＞f(1)恒成立，求m的取值范围．

查看答案和解析>>

练习册

高中

初中

小学

设m＜0.点M答案解析

设m＜0，角α的终边经过点P（-3m，4m），那么sinα+2cosα的值等于________．