如图 在正三角形ABC中 def分别是BC AC AB上的点答案解析
科目:czsx
来源:2016届山东德州十五中九年级第二次模拟检测数学试卷(解析版)
题型:选择题
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )

A.1∶3 B.2∶3 C. ∶2 D.
∶2 D. ∶3
∶3
查看答案和解析>>
科目:czsx
来源:
题型:
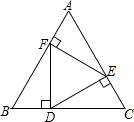
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于________.
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于________.
查看答案和解析>>
科目:czsx
来源:汉沽区一模
题型:填空题
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于______.
查看答案和解析>>
科目:czsx
来源:2010-2011学年浙江省衢州市菁才中学九年级(上)第三次月考数学试卷(解析版)
题型:填空题
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
.

查看答案和解析>>
科目:czsx
来源:2012年天津市汉沽区中考数学一模试卷(解析版)
题型:填空题
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
.

查看答案和解析>>
科目:czsx
来源:2012年浙江省杭州市中考数学模拟试卷(50)(解析版)
题型:填空题
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
.

查看答案和解析>>
科目:czsx
来源:浙江省中考真题
题型:单选题
如图,在正三角形ABC中,D、E、F分别是BC、AC、AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
A.1∶3
B.2∶3
C.
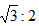
D.
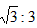
查看答案和解析>>
科目:czsx
来源:2009年浙江省湖州市中考数学试题
题型:013
如下图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于
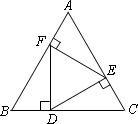
[ ]
C. ∶2
∶2
D. ∶3
∶3
查看答案和解析>>
科目:czsx
来源:专项题
题型:单选题
如图所示,在正三角形ABC中,D,E,F分 别是BC,AC,AB上的点,DE⊥AC,EF⊥ AB,FD⊥BC,则△DEF的面积与△ABC 的面积之比等于
A.1∶3
B.2∶3
C.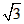 ∶2
∶2
D.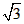 ∶3
∶3
查看答案和解析>>
科目:gzsx
来源:北京模拟题
题型:解答题
如图所示,正三角形ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角E-DF-C的余弦值;
(3)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。
查看答案和解析>>
科目:czsx
来源:2015届浙江慈溪育才中学八年级上学期第二次月考数学试卷(解析版)
题型:解答题
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B.点C重合).

(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B.点C重合).
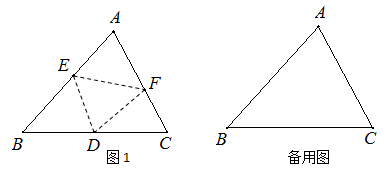
(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
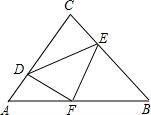
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
①CD=BE
②四边形CDFE不可能是正方形
③△DEF是等腰直角三角形
④
S四边形CDFE=S△ABC.当∠DFE在△ABC内绕顶点F旋转时(点D不与A,C重合),
上述结论中始终正确的有
①③④
①③④
.
查看答案和解析>>
科目:czsx
来源:
题型:
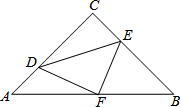
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC上运动(点E不与A、C重合),且保持AE=CF,连接DE、DF、EF,在运动变化过程中,有下列结论:
①△DEF是等腰三角形;
②四边形CEDF不可能是正方形;
③四边形CEDF的面积随点E位置改变而发生变化;
④点C到线段EF的最大距离为
;
⑤AE
2+BF
2=EF
2;
⑥EF=
DF.
其中结论正确的是
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B、点C重合),
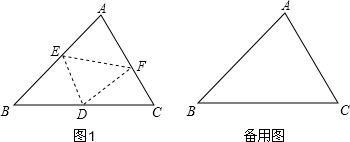
(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:填空题
 如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①△DEF是等腰直角三角形
②四边形CEDF不可能为正方形
③四边形CEDF的面积随点E位置的改变而发生变化
④点C到线段EF的最大距离为
其中正确的有________(填上你认为正确结论的所有序号)
查看答案和解析>>
科目:czsx
来源:
题型:

(2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
①△DEF是等腰直角三角形
②四边形CEDF不可能为正方形
③四边形CEDF的面积随点E位置的改变而发生变化
④点C到线段EF的最大距离为
其中正确的有
①④
①④
(填上你认为正确结论的所有序号)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
2.请从以下A、B两题中任选一题解答,若两题都做,按A题给分.
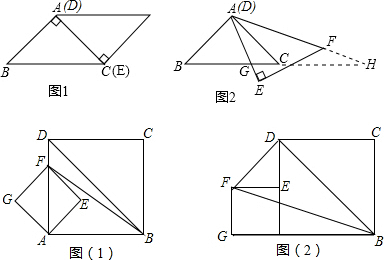
A.如图1,△ABC和△FED均为等腰直角三角形,AC与BE重合,AB=AC=EF=3,∠BAC=∠DEF=90°,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB重合时,旋转停止.现不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图2.
(1)始终与△AGC相似的三角形是△HAB和△HGA;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图2的情形说明理由);
(3)在整个旋转过程中,当旋转角为多少度时,△AGH是等腰三角形?请直接写出旋转的度数.
B.如图(1),正方形AEFG的边长为1,正方形ABCD的边长为3,且点F在AD上;
(1)求S
△DBF;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得到图(2)中的S
△DBF;
(3)将正方形AEFG绕点A旋转一周,在旋转的过程中,S
△DBF存在最大值与最小值,请直接写出最大值为$\frac{15}{2}$,最小值为$\frac{3}{2}$.
我选做的是A题.
查看答案和解析>>


 ∶2 D.
∶2 D. ∶3
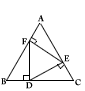
∶3  如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于________.
如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于________.



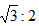
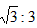

![]() ∶2
∶2![]() ∶3
∶3
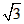 ∶2
∶2  ∶3
∶3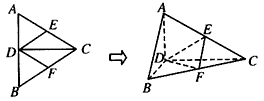


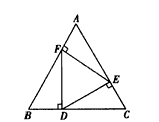
 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DEF是等腰直角三角形;②四边形CDFE可能为正方形;③DE长度的最小值为4;④四边形CDFE的面积保持不变;⑤△CDE面积的最大值为8.其中正确的结论是 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC上运动(点E不与A、C重合),且保持AE=CF,连接DE、DF、EF,在运动变化过程中,有下列结论:
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC上运动(点E不与A、C重合),且保持AE=CF,连接DE、DF、EF,在运动变化过程中,有下列结论:
 如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
 (2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
(2013•昆都仑区一模)如图所示,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A,C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论: