科目:czsx
来源:
题型:解答题
在等边三角形ABC中,D、E分别为AB、BC延长线上的点,且BD=CE,AE交DC的延长线于点F,A G⊥CD,垂足为G.
G⊥CD,垂足为G.
求证:(1)△ACE≌△CBD;(2)AF=2FG.
查看答案和解析>>
科目:czsx
来源:
题型:
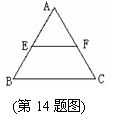
如图,在等边三角形ABC中,点E、F分别是AB、AC的中点,EF =4,△ABC的周长为____ .
查看答案和解析>>
科目:czsx
来源:
题型:

19、在等边三角形ABC中,D、E分别为AB、BC延长线上的点,且BD=CE,AE交DC的延长线于点F,AG⊥CD,垂足为G.
求证:(1)△ACE≌△CBD;(2)AF=2FG.
查看答案和解析>>
科目:czsx
来源:
题型:
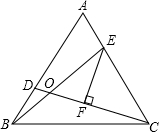
已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.
已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.
查看答案和解析>>
科目:czsx
来源:2012年5月中考数学模拟试卷(5)(解析版)
题型:解答题
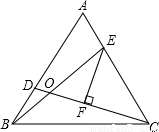
已知在等边三角形ABC中,D、E分别为AB、AC上的点,且BD=AE,EB与CD相交于点O,EF⊥CD于点F.求证:OE=2OF.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且AD=BE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:AF=2FG.
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且AD=BE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:AF=2FG.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且AD=BE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:AF=2FG.
查看答案和解析>>
科目:czsx
来源:
题型:
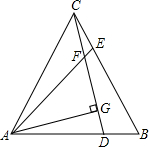
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:
(1)△ACE≌△CBD;
(2)AF=2FG.
查看答案和解析>>
科目:czsx
来源:
题型:
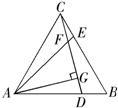
26、如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且AD=BE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:AF=2FG.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
2.
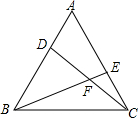
如图,在等边三角形ABC中,D、E分别为AB、BC边上的两点,且AD=CE,求证:∠EBA=∠DCB.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
3.

已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:
(1)△ACD≌△BAE;
(2)BP=2PQ.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
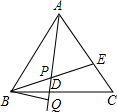 已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:月考题
题型:证明题
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:
题型:
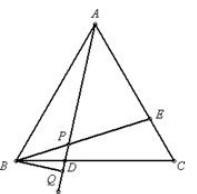
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连 结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:2012-2013学年江西省九江市彭泽县新星学校九年级(上)月考数学试卷(9月份)(解析版)
题型:解答题
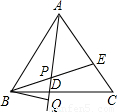
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:2011-2012学年双湖中学九年级(上)月考数学试卷(解析版)
题型:解答题
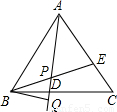
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
查看答案和解析>>
科目:czsx
来源:2010-2011学年北师大版九年级(上)第一次段考数学试卷(1-3章)(解析版)
题型:解答题
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.

查看答案和解析>>
科目:czsx
来源:2011-2012学年辽宁省本溪市九年级(上)第一次质量测试数学试卷(解析版)
题型:解答题
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.

查看答案和解析>>

 G⊥CD,垂足为G.
G⊥CD,垂足为G. 19、在等边三角形ABC中,D、E分别为AB、BC延长线上的点,且BD=CE,AE交DC的延长线于点F,AG⊥CD,垂足为G.
19、在等边三角形ABC中,D、E分别为AB、BC延长线上的点,且BD=CE,AE交DC的延长线于点F,AG⊥CD,垂足为G.
 如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证:
如图,在等边三角形ABC中,D、E分别为AB、BC上的点,且BD=CE,AE、CD相交于点F,AG⊥CD,垂足为G.求证: 已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:
已知:在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连结AD、BE交于点P,作BQ⊥AD,垂足为Q.求证: 已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.
已知:如图,在等边三角形ABC中,D、E分别为BC、AC上的点,且AE=CD,连接AD、BE交于点P,作BQ⊥AD,垂足为Q.求证:BP=2PQ.




