科目：gzsx 来源： 题型：
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
科目：gzsx 来源： 题型：044
已知a>0，函数f（x）=ax－bx2.
（1）当b>0时，若对任意x∈R都有f（x）≤1，证明a≤2
；
（2）当b>1时，证明：对任意x∈［0，1］，|f（x）|≤1的充要条件是b－1≤a≤2
；
（3）当0<b≤1时，讨论：对任意x∈［0，1］，|f（x）|≤1的充要条件.
科目：gzsx 来源：数学教研室 题型：044
（1）当b>0时，若对任意x∈R都有f（x）≤1，证明a≤2
；
（2）当b>1时，证明：对任意x∈［0，1］，|f（x）|≤1的充要条件是b－1≤a≤2
；
（3）当0<b≤1时，讨论：对任意x∈［0，1］，|f（x）|≤1的充要条件.
科目：gzsx 来源： 题型：044
(1)当b＞0时,若对任意x∈R都有f(x)≤1,证明a≤
;
(2)当0＜b≤1时,讨论:对任意x∈［0,1］,|f(x)|≤1的充要条件.
科目：gzsx 来源：湖南省长沙市第一中学2011届高三第三次月考文科数学试题 题型：044
已知a≠0，函数f(x)＝
a2x3－ax2＋
，g(x)＝－ax＋1，x∈R．
(Ⅰ)求函数f(x)的单调递减区间；
(Ⅱ)若在区间(0，
]上至少存在一个实数x0，使f(x0)＞g(x0)成立，试求正实数a的取值范围．
科目：gzsx 来源： 题型：
(1)当b＞0时,若对任意x∈R都有f(x)≤1,证明a≤
;
(2)当0＜b≤1时,讨论:对任意x∈［0,1］,|f(x)|≤1的充要条件.
科目：gzsx 来源： 题型：
已知a>0，函数f(x)=ax-bx2,
（1）当b>0时，若对任意x∈R都有f(x)≤1，证明：a≤2
；
（2）当b>1时，证明：对任意x∈[0, 1], |f(x)|≤1的充要条件是：b-1≤a≤2；
（3）当0<b≤1时，讨论：对任意x∈[0, 1], |f(x)|≤1的充要条件。
科目：gzsx 来源： 题型：
已知a>0，函数f(x)＝ax2＋bx＋c.
若x0满足关于x的方程2ax＋b＝0，则下列选项的命题中为假命题的是 ( )
A．∃x∈R，f(x)≤f(x0) B．∃x∈R，f(x)≥f(x0)
C．∀x∈R，f(x)≤f(x0) D．∀x∈R，f(x)≥f(x0)
科目：gzsx 来源：不详 题型：解答题
；；科目：gzsx 来源：蓝山县模拟 题型：解答题
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
科目：gzsx 来源： 题型：
已知a>0，函数f（x）=ax－bx2.
（1）当b>0时，若对任意x∈R都有f（x）≤1，证明a≤2
；
（2）当b>1时，证明：对任意x∈［0，1］，|f（x）|≤1的充要条件是b－1≤a≤2；
（3）当0<b≤1时，讨论：对任意x∈［0，1］，|f（x）|≤1的充要条件.
科目：gzsx 来源： 题型：
已知a>0，函数f(x)=ax－bx2,
（1）当b>0时，若对任意x∈R都有f(x)≤1，证明：a≤2
；
（2）当b>1时，证明：对任意x∈[0, 1], |f(x)|≤1的充要条件是：b－1≤a≤2；
（3）当0
科目：gzsx 来源： 题型：
(1)当b＞0时,若对任意x∈R都有f(x)≤1,证明a≤2
；
(2)当b＞1时,证明对任意x∈［0,1］,|f(x)|≤1的充要条件是b-1≤a≤2
；
(3)当0＜b≤1时,讨论:对任意x∈［0,1］,|f(x)|≤1的充要条件.
科目：gzsx 来源： 题型：
(1)当b＞0时,若对任意x∈R都有f(x)≤1,证明
;
(2)当b＞1时,证明对任意x∈［0,1］,|f(x)|≤1的充要条件是b-1≤a≤
;
(3)当0＜b≤1时,讨论:对任意x∈［0,1］,|f(x)|≤1的充要条件.
科目：gzsx 来源： 题型：
(1)当b＞0时，若对任意x∈R都有f(x)≤1,证明a≤2b;
(2)当b＞1时，证明对任意x∈［0,1］,|f(x)|≤1的充要条件是b-1≤a≤2
.
科目：gzsx 来源：专项题 题型：单选题
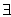x∈R，f（x）≤f（x0）
x∈R，f（x）≥f（x0）
x∈R，f（x）≤f（x0）x∈R，f（x）≥f（x0）科目：gzsx 来源： 题型：
（本小题16分）已知a>0，函数f（x）=ax－bx2.
（I）当b>0时，若对任意x∈R都有f（x）≤1，证明a≤2
；
（II）当b>1时，证明：对任意x∈［0，1］，|f（x）|≤1的充要条件是b－1≤a≤2；
（III）当0<b≤1时，讨论：对任意x∈［0，1］，|f（x）|≤1的充要条件.
科目：gzsx 来源： 题型：解答题
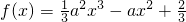，g（x）=-ax+1，x∈R．
上至少存在一个实数x0，使f（x0）＞g（x0）成立，试求正实数a的取值范围．科目：gzsx 来源：月考题 题型：解答题
，g（x）=﹣ax+1，x∈R．
上至少存在一个实数x0，使f（x0）＞g（x0）成立，