
科目:czsx 来源: 题型:解答题

科目:czsx 来源:2006年山东省日照市中等学校招生考试数学试题 题型:059
阅读下面的材料:
如图,在以AB为直径的半圆O内有一点P,AP、BP的延长线分别交半圆O于点C、D.求证:AP·AC+BP·BD=AB2.
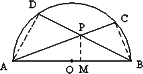
证明:连结AD、BC,过P作PM⊥AB,则∠ADB=∠AMP=90°,
∴点D、M在以AP为直径的圆上;同理:M、C在以BP为直径的圆上.
由割线定理得:AP·AC=AM·AB,BP·BD=BM·BA,
所以,AP·AC+BP·BD=AM·AB+BM·AB=AB·(AM+BM)=AB2.
当点P在半圆周上时,也有AP·AC+BP·BD=AP2+BP2=AB2成立,那么:
(1)如图当点P在半圆周外时,结论AP·AC+BP·BD=AB2是否成立?为什么?
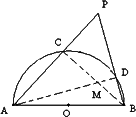
(2)如图当点P在切线BE外侧时,你能得到什么结论?将你得到的结论写出来.
科目:gzsx 来源:2012-2013学年河北省石家庄市高三下学期第二次质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1几何证明选讲
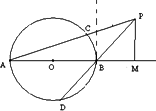
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为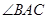 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
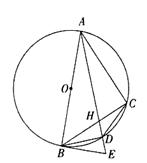
(I )求证:BD平分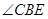
(II)求证:AH.BH=AE.HC
科目:gzsx 来源:2012-2013学年河北省石家庄市高三下学期第二次质量检测文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为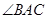 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.

(I )求证:BD平分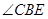
(II)求证:AH?BH=AE?HC
科目:gzsx 来源: 题型:解答题
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为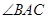 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分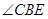
(II)求证:AH.BH=AE.HC
科目:gzsx 来源: 题型:解答题
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为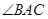 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分
(II)求证:AH•BH=AE•HC
科目:gzsx 来源:不详 题型:解答题
 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.

科目:czsx 来源: 题型:
 延长线与直线AE交于C点.
延长线与直线AE交于C点.| 1 | 2 |
科目:czsx 来源: 题型:
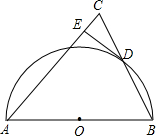 D=BD,过点D作半圆O的切线交AC于E点.
D=BD,过点D作半圆O的切线交AC于E点.科目:czsx 来源: 题型:
 如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点.C、D在直径AB的两侧.
如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点.C、D在直径AB的两侧.科目:czsx 来源:2007中考夺标冲刺模拟题(新课标)(八)、数学 题型:044
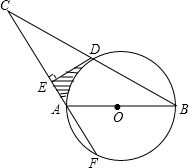
如图,AB是⊙O的直径,过圆上一点D作⊙O的切线DE,与过点A的直线垂直于E,弦BD的延长线与直线AE交于C点.
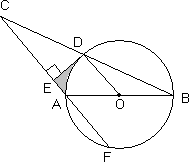
(1)求证:点D为BC的中点;
(2)设直线EA与⊙O的另一交点为F,求证:CA2-AF2=4CE·EA;
(3)若弧AD=![]() ,⊙O的半径为r.求由线段DE、AE和
,⊙O的半径为r.求由线段DE、AE和![]() 所围成的阴影部分的面积.
所围成的阴影部分的面积.
科目:czsx 来源: 题型:解答题
 如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点.C、D在直径AB的两侧.
如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点.C、D在直径AB的两侧.科目:czsx 来源: 题型:解答题
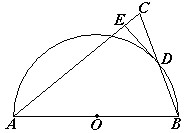
 D=BD,过点D作半圆O的切线交AC于E点.
D=BD,过点D作半圆O的切线交AC于E点.科目:czsx 来源:四川省中考真题 题型:解答题
科目:czsx 来源:第24章《圆(下)》中考题集(15):24.2 圆的切线(解析版) 题型:解答题

科目:czsx 来源:第35章《圆(二)》中考题集(15):35.3 探索切线的性质(解析版) 题型:解答题

科目:czsx 来源:第3章《圆》中考题集(40):3.2 点、直线与圆的位置关系,圆的切线(解析版) 题型:解答题
科目:czsx 来源:第28章《圆》中考题集(48):28.2 与圆有关的位置关系(解析版) 题型:解答题

科目:czsx 来源:第3章《直线与圆、圆与圆的位置关系》中考题集(14):3.1 直线与圆的位置关系(解析版) 题型:解答题
