
科目:gzwl 来源: 题型:
在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正。一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向。则
(1)粒子进入磁场后做圆周运动的半径是多大?
(2)若O、P连线与x轴之间的夹角为45°,则磁场变化的周期T为多大?
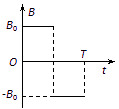 (3)因P点的位置随着磁场周期的变化而变化,试求P点的纵坐标的最大值为多少?
(3)因P点的位置随着磁场周期的变化而变化,试求P点的纵坐标的最大值为多少?
科目:gzwl 来源:泰州模拟 题型:问答题

科目:gzwl 来源: 题型:
在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正。一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向。则
(1)粒子进入磁场后做圆周运动的半径是多大?
(2)若O、P连线与x轴之间的夹角为45°,则磁场变化的周期T为多大?
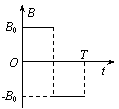 (3)因P点的位置随着磁场周期的变化而变化,试求P点的纵坐标的最大值为多少?
(3)因P点的位置随着磁场周期的变化而变化,试求P点的纵坐标的最大值为多少?
科目:gzwl 来源:2010-2011学年江西省赣州市南康市潭口中学高二(上)期中物理试卷(解析版) 题型:解答题
 在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则
在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则科目:gzwl 来源:2010年江苏省连云港市高考物理二模试卷(解析版) 题型:解答题
 在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则
在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则科目:gzwl 来源:2009-2010学年江苏省南通、泰州、扬州高三(下)期初调研物理试卷(解析版) 题型:解答题
 在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则
在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则科目:gzwl 来源:不详 题型:计算题

科目:czsx 来源: 题型:
在数学活动课上,老师提出了一个问题,希望同学们进行探究.
在平面直角坐标系中,若一次函数 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象交于C、D两点,则AD和BC有怎样的数量关系?
的图象交于C、D两点,则AD和BC有怎样的数量关系?
同学们通过合作讨论,逐渐完成了对问题的探究.
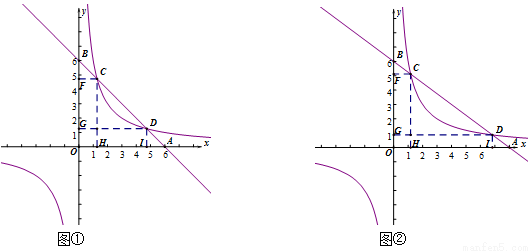
小勇说:我们可以从特殊入手,取 进行研究(如图①),此时我发现AD=BC.
进行研究(如图①),此时我发现AD=BC.
小攀说:在图①中,分别从点C、D两点向两条坐标轴作垂线,根据所学知识可以知道有两个图形的面积是相等的,并能求出确定的值,而且在图②中,此时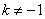 ,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
小高说:我还发现,在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是 .


图① 图②

(1)请完成以上填空;
(2)请结合以上三位同学的讨论,对图②所示的情况下,证明AD=BC;
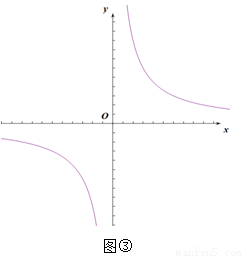
小峰突然提出一个问题:通过刚才的证明,我们可以知道当直线与双曲线的两个交点都在第一象限时, 总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
(3)请你结合小峰提出的问题,在图③中画出示意图,并判断结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
科目:czsx 来源:2016届北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
在数学活动课上,老师提出了一个问题,希望同学们进行探究.
在平面直角坐标系中,若一次函数 的图象与x轴交于点A,与y轴交于点B,与反比例函数
的图象与x轴交于点A,与y轴交于点B,与反比例函数 的图象交于C、D两点,则AD和BC有怎样的数量关系?
的图象交于C、D两点,则AD和BC有怎样的数量关系?
同学们通过合作讨论,逐渐完成了对问题的探究.
小勇说:我们可以从特殊入手,取 进行研究(如图①),此时我发现AD=BC.
进行研究(如图①),此时我发现AD=BC.
小攀说:在图①中,分别从点C、D两点向两条坐标轴作垂线,根据所学知识可以知道有两个图形的面积是相等的,并能求出确定的值,而且在图②中,此时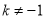 ,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
,这一结论仍然成立,即_______的面积=_______的面积,此面积的值为____.
小高说:我还发现,在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是 .
(1)请完成以上填空;
(2)请结合以上三位同学的讨论,对图②所示的情况下,证明AD=BC;
小峰突然提出一个问题:通过刚才的证明,我们可以知道当直线与双曲线的两个交点都在第一象限时, 总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
(3)请你结合小峰提出的问题,在图③中画出示意图,并判断结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
科目:czsx 来源:数学教研室 题型:044
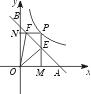
(1)写出E、F两点的坐标(用含有a ,b的代数式表示);
(2)求△OEF的面积;
(3)若P点在y=![]() 的图象上移动,则∠EOF的大小是否变化,并说明理由.
的图象上移动,则∠EOF的大小是否变化,并说明理由.
科目:czsx 来源: 题型:解答题
科目:gzwl 来源: 题型:阅读理解
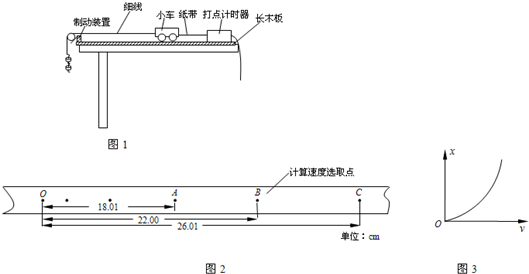
| h2 |
| h1 |
| h2 |
| h1 |
| 1 |
| v |
科目:gzwl 来源: 题型:阅读理解
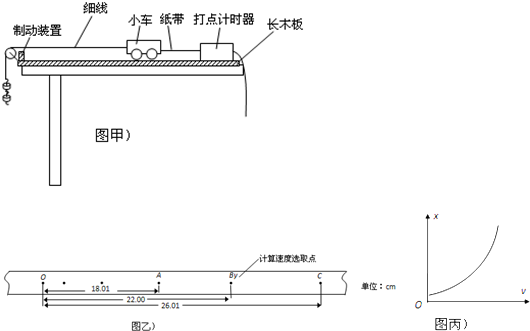
| h2 |
| h1 |
| h2 |
| h1 |
| 1 |
| v |
科目:gzwl 来源:高三物理第二轮复习易错题系列 力学题 题型:038
如图甲所示,在xOy平面第Ⅰ象限内,有一个匀强磁场,磁感应强度大小恒定为B0,方向垂直于xOy,且随时间作周期性变化,如图乙所示.规定垂直xOy平面向里的磁场方向为正,一个质量为m,电量为q的正粒子,在t=0时刻从坐标原点以速度v0沿x轴正方向射入,在匀强磁场中运动,运动中带电粒子只受洛伦兹力作用,经过一个磁场变化周期T(未确定),粒子到达第Ⅰ象限内某一点P,且速度方向沿x轴正方向.
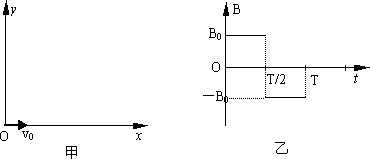
(1)若O、P连线与x轴之间的夹角为45°,则磁场的变化周期T是多大?
(2)因P点的位置随磁场周期的变化而变动,试求P点的纵坐标的最大值是多少?
科目:czsx 来源: 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用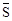 表示,例如图1中,
表示,例如图1中,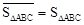 ,图2中,
,图2中,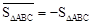 .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组(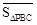 ,
,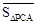 ,
,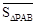 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作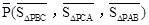 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,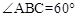 ,则
,则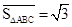 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”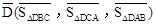 为
为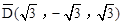 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: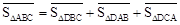 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则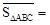 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系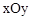 中,点
中,点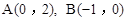 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为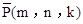 ,
,
试探究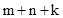 与
与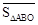 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点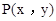 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于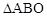 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点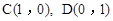 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.
科目:czsx 来源:不详 题型:解答题
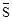 表示,例如图1中,
表示,例如图1中,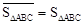 ,图2中,
,图2中,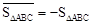 .
.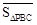 ,
,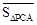 ,
,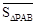 )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作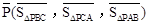 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2,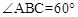 ,则
,则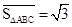 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标”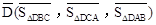 为
为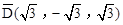 .在图3中,我们知道
.在图3中,我们知道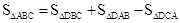 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: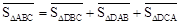 .
.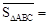 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现: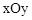 中,点
中,点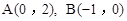 ,
, 的“面积坐标”为
的“面积坐标”为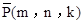 ,
,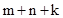 与
与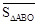 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;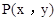 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于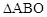 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);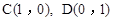 ,点Q在抛物线
,点Q在抛物线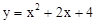 上,求当
上,求当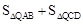 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.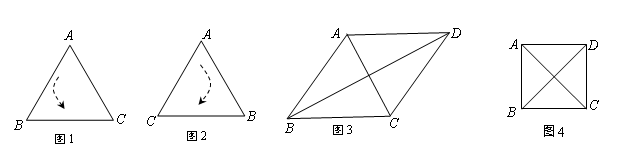
科目:czsx 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
定义1:在△ABC中,若顶点A,B,C按逆时针方向排列,则规定它的面积为“有向面积”;若顶点A,B,C按顺时针方向排列,则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用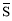 表示,例如图1中,
表示,例如图1中,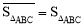 ,图2中,
,图2中, .
.
定义2:在平面内任取一个△ABC和点P(点P不在△ABC的三边所在直线上),称有序数组( ,
, ,
, )为点P关于△ABC的“面积坐标”,记作
)为点P关于△ABC的“面积坐标”,记作 ,例如图3中,菱形ABCD的边长为2,
,例如图3中,菱形ABCD的边长为2, ,则
,则 ,点G关于△ABC的“面积坐标”
,点G关于△ABC的“面积坐标” 为
为 .在图3中,我们知道
.在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为: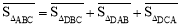 .
.
应用新知:
(1)如图4,正方形ABCD的边长为1,则 ,点D关于△ABC的“面积坐标”是 ;探究发现:
,点D关于△ABC的“面积坐标”是 ;探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
,
①若点P是第二象限内任意一点(不在直线AB上),设点P关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点P关于
是第四象限内任意一点,请直接写出点P关于 的“面积坐标”(用x,y表示);
的“面积坐标”(用x,y表示);
解决问题:
(3)在(2)的条件下,点 ,点Q在抛物线
,点Q在抛物线 上,求当
上,求当 的值最小时,点Q的横坐标.
的值最小时,点Q的横坐标.

科目:czsx 来源: 题型:
. |
| S |
. |
| S △ABC |
. |
| S △ABC |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| P |
. |
| S △PBC |
. |
| S △PCA |
. |
| S △PAB |
. |
| S △ABC |
| 3 |
. |
| D |
. |
| S △DBC |
. |
| S △DCA |
. |
| S △DAB |
. |
| D |
| 3 |
| 3 |
| 3 |
. |
| S △ABC |
. |
| S △DBC |
. |
| S △DAB |
. |
| S △DCA |
. |
| S △ABC |
. |
| P |
. |
| S △ABO |

科目:czsx 来源: 题型:
定义1:在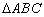 中,若顶点
中,若顶点 ,
, ,
, 按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
 ,
, ,
, 按顺时针方向排列,则规定它的面积的相反数为
按顺时针方向排列,则规定它的面积的相反数为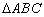 的“有向面积”。“有
的“有向面积”。“有 向面积”用
向面积”用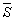 表示,
表示,


 例如图1中,
例如图1中, ,图2中,
,图2中,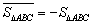 。
。
定义2:在平面内任取一个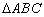 和点
和点 (点
(点 不在
不在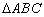 的三边所在直线上),称有序数组(
的三边所在直线上),称有序数组( ,
, ,
,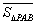 )为点
)为点 关于
关于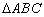 的“
的“ 面积坐标”,记作
面积坐标”,记作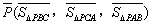 ,例如图3中,菱形
,例如图3中,菱形 的边长为2,
的边长为2, ,则
,则 ,点
,点 关于
关于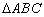 的“面积坐标”
的“面积坐标” 为
为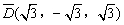 。
。
 在图3中,我们知道
在图3中,我们知道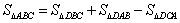 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为:
 。
。
应用新知:
(1)如图4,正方形 的边长为1,则
的边长为1,则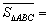 ,点
,点 关于
关于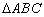 的“面积坐标”是 ;
的“面积坐标”是 ;
探究发现:
(2)在平面直角坐标系 中,点
中,点 ,
, .
.
①若点 是第二象限内任意一点(不在直线
是第二象限内任意一点(不在直线 上),设点
上),设点 关于
关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究 与
与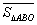 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点
是第四象限内任意一点,请直接写出点 关于
关于 的“面积坐标”(用
的“面积坐标”(用 表示);
表示);
解决问题:
(3)在(2)的条件下,点 ,
, ,点
,点 在抛物线
在抛物线 上,求当
上,求当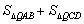 的值最小时,点
的值最小时,点 的横坐标。
的横坐标。
科目:gzwl 来源: 题型:
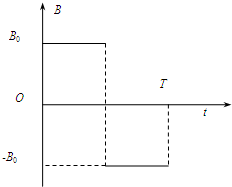 (2010•泰州模拟)在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则
(2010•泰州模拟)在坐标系xOy平面的第一象限内,有一个匀强磁场,磁感应强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图所示,规定垂直xOy平面向里的磁场方向为正.一个质量为m,电荷量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,不计重力的影响,经过一个磁场变化周期T(未确定)的时间,粒子到达第Ⅰ象限内的某点P,且速度方向仍与x轴正方向平行同向.则