
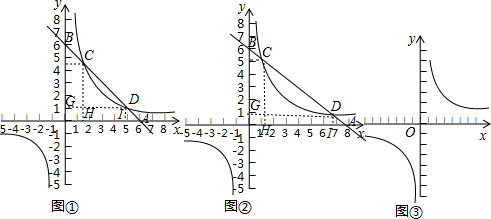
分析 (1)根据题目的叙述即可直接解答;
(2)连接GH,GC,DH,证明S△CGH=S△GHD.则CD∥GH,然后根据平行四边形的性质求解;
(3)与(2)解法相同,证明S△CGH=S△GHD.则点C,D到GH的距离相等,然后利用平行四边形的性质证得.
解答 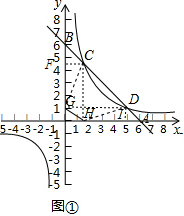 解:(1)S矩形FCHO=S矩形GDIO,这一结论仍然成立,即的四边形OHCF面积=四边形OIDG的面积,此面积的值为6.
解:(1)S矩形FCHO=S矩形GDIO,这一结论仍然成立,即的四边形OHCF面积=四边形OIDG的面积,此面积的值为6.
在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是GH.
故答案是:四边形OHCF,四边形OIDG,6,GH;
(2)成立,证明如下:
如图①,连接GH,GC,DH,
∵点C,D是反比例图象上的点,
∴S矩形FCHO=S矩形GDIO.
∴$\frac{1}{2}{S_{矩形FCHO}}=\frac{1}{2}{S_{矩形GDIO}}$.
∴S△CGH=S△GHD.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BCHG和四边形GHAD都是平行四边形.
∴BC=GH,GH=DA.
即AD=BC;
(3)画出图形,得到GH,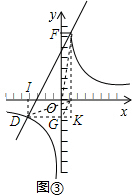
∵点C,D是反比例图象上的点,
∴S矩形FCHO=S矩形GDIO.
∴$\frac{1}{2}{S_{矩形FCHO}}=\frac{1}{2}{S_{矩形GDIO}}$.
∴S△CGH=S△GHD.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BCHG和四边形GHAD都是平行四边形.
∴BC=GH,GH=DA.
即AD=BC.
点评 本题考查了反比例函数的性质以及反比例函数比例系数k的几何意义,注意题目之间的联系是解决本题的关键.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.
如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时间x(周) | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 每千克售价y(元) | 30 | 28 | 26 | 24 | 22 | 20 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 100 |
| 不及格 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )| A. | ∠COE | B. | ∠AOF | C. | ∠DOB | D. | ∠EOF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com