
科目:czsx 来源: 题型:解答题


科目:czsx 来源: 题型:
观察并探求下列各问题,写出你所观察得到的结论,并说明理由.
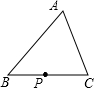
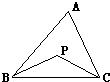
(1)如图①,△ABC中,P为边BC上一点,试观察比较BP+PC与AB+AC的大小,并说明理由.
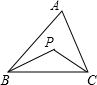
(2)将(1)中点P移至△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.
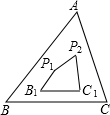
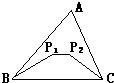
(3)将(2)中点P变为两个点P1、P2得图③,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
(4)将(3)中的点P1、P2移至△ABC外,并使点P1、P2与点A在边BC的异侧,且∠P1BC<∠ABC,∠P2CB<∠ACB,得图④,试观察比较四边形BP1P2C的周长与△ABC的周长的大小,并说明理由.
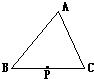
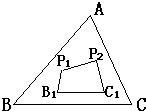
(5)若将(3)中的四边形BP1P2C的顶点B、C移至△ABC内,得四边形B1P1P2C1,如图⑤,试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小,并说明理由.

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:解答题

科目:czyw 来源:语文教研室 题型:048
有一天,两个强盗闯进了圆明园。一个强盗洗劫,另一个强盗放火。似乎得胜之后,便可以动手行窃了。对圆明园进行了大规模的劫掠,赃物由两个胜利者均分。我们看到,这整个事件还与额尔金的名字有关,这名字又使人不能不忆起巴特农神庙。从前对巴特农神庙怎么干,现在对圆明园也怎么干,只是更彻底,更漂亮,以至于荡然无存。我们所有大教堂的财宝加在一起,也许还抵不上东方这座了不起的富丽堂皇的博物馆。那儿不仅仅有艺术珍品,还有大堆的金银制品。丰功伟绩!收获巨大!两个胜利者,一个塞满了腰包,这是看得见的,另一个装满了箱箧。他们手挽手,笑嘻嘻地回到了欧洲。这①就是这②两个强盗的故事。
我们欧洲人是文明人,中国人在我们眼中是野蛮人。这就是文明对野蛮所干的事情。
1.文中的两个“强盗”指_______________,作者之所以称他们“强盗”的原因是(请用段中的话回答):______________________________________________________________
2.第一节加点的“闯”能否换成“走”?为什么?
答:________________________________________________________________________
3.“对圆明园进行了大规模的劫掠”中“大规模”能否删去?为什么?根据语段中提供的材料,说说两个强盗是怎么破坏圆明园的。
答:________________________________________________________________________
________________________________________________________________________
4.语段中提到巴特农神庙的作用是什么?
答:________________________________________________________________________
5.“我们所有大教堂的财宝加在一起,也许还抵不上东方这座了不起的富丽堂皇的博物馆”中的“也许”能否删去?为什么?
答:________________________________________________________________________
________________________________________________________________________
6.“富丽堂皇”和“丰功伟绩”这两个短语的感情色彩在语段中是否相同?请结合课文,作简要解析。
答:________________________________________________________________________
________________________________________________________________________
7.指出文中加点的三个代词所指代的内容。
(1)那儿:___________________________________________________________________
(2)这①:___________________________________________________________________
(3)这②:___________________________________________________________________
8.请分别用两个成语,指出下列句子中加点词语的言外之意。
文中句子:他们手挽手,笑嘻嘻地回到了欧洲。
“手挽手”言外之意是:__________;“笑嘻嘻”言外之意是:_________________。
9.第二节的表达方式是______________;运用的主要修辞手法是____________,运用这种修辞手法的作用是
_______________________________________________________________。
10.中国当年被英法等列强一再欺凌,乃至受到大规模劫掠的原因是什么?
科目:czyw 来源:语文教研室 题型:048
二十日夜起,长江北岸人民解放军中路军首先突破安庆、芜湖线,渡至繁昌、铜陵、青阳、获港、鲁港地区,二十四小时内即已渡过三十万人。二十一日下午五时起,我西路军开始渡江,地点在九江、安庆段。至发电时止,该路三十五万人民解放军已渡过三分之二,余部二十三日可渡完。这一路现已占领贵池、殷家汇、东流、至德、彭泽之线的广大南岸阵地,正向南扩展中。和中路军所遇敌情一样,我西路军当面之敌亦纷纷溃退,毫无斗志,我军所遇之抵抗,甚为微弱。此种情况,一方面由于人民解放军英勇善战,锐不可当;另一方面,这和国民党反动派拒绝签订和平协定,有很大关系。国民党的广大官兵一致希望和平,不想再打了,听见南京拒绝和平,都很泄气。战犯汤恩伯二十一日到芜湖督战,不起丝毫作用。汤恩伯认为南京江阴段防线是很巩固的,弱点只存在于南京九江一线。不料正是汤恩伯到芜湖的那一天,东面防线又被我军突破了。我东路三十五万大军与西路同日同时发起渡江作战。所有预定计划,都已实现。至发电时止,我东路各军已大部渡过南岸,余部二十三日可以渡完。此处敌军抵抗较为顽强,然在二十一日下午至二十二日下午的整天激战中,我已歼灭及击溃一切抵抗之敌,___________扬中、镇江、江阴诸县的广大地区,并___________江阴要塞,_____________长江。我军前锋,业已_____________镇江无锡段铁路线。
1.在语段中的四处横线上填上合适的动词。
2.从结构上看,语段是消息的________________部分。
3.加点的“至发电时止”说明_____________________________________________________
4.加点的“此种情况”是指_______________________________________________________
5.语段中加点的“只”是____________词,它突出了汤恩伯__________________________。
6.加点的“不料正是汤恩伯到芜湖的那一天”能否换成“结果就在二十一日那一天”?为什么?
答:_________________________________________________________________________
_________________________________________________________________________
7.“听见南京拒绝和平,都很泄气”中的“南京”能否写成“南京蒋介石政府”?为什么?
答:_________________________________________________________________________
8.把语段分成三个层次,并概括各层次的段落大意。
第一层____________________________至________________________________________
层次大意是:________________________________________________________________
第二层____________________________至________________________________________
层次大意是:________________________________________________________________
第三层____________________________至________________________________________
层次大意是:________________________________________________________________
9.该语段的主要意思是:________________________________________________________
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:填空题
科目:czsx 来源:2010年海南省中考数学模拟试卷(3)(解析版) 题型:填空题
科目:czsx 来源: 题型:
问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】
如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】
如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(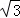 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: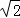 =1.41,
=1.41,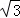 =1.73)
=1.73)
科目:czsx 来源:2016届江苏省南京市溧水区中考一模数学试卷(解析版) 题型:解答题
问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.

(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
科目:czsx 来源:2016届江苏省九年级下第一次调研数学试卷(解析版) 题型:解答题
问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.

【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF= 米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: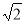 =1.41,
=1.41,  =1.73)
=1.73)
科目:czsx 来源:2016届河南省中考模拟(一)数学试卷(解析版) 题型:解答题
问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足________________关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(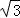 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: =1.41,
=1.41,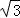 =1.73)
=1.73)

科目:czsx 来源:2013年江苏省南京市鼓楼区中考一模数学试卷(带解析) 题型:解答题
【问题提出】
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
【初步思考】
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
【深入探究】
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;
Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;
Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图, .
求证: .
证明:
(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形 和四边形
和四边形 为例,分为以下四类:
为例,分为以下四类:
①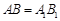 ,
, ,
, ,
, ,
, ;
;
②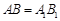 ,
, ,
, ,
, ,
,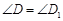 ;
;
③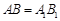 ,
, ,
, ,
, ,
,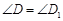 ;
;
④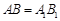 ,
, ,
, ,
, ,
, ;
;
其中能判定四边形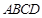 和四边形
和四边形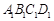 全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
科目:czsx 来源:2013年江苏省南京市鼓楼区中考一模数学试卷(解析版) 题型:解答题
【问题提出】
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
【初步思考】
在两个四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
【深入探究】
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;
Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;
Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图, .
求证: .
证明:
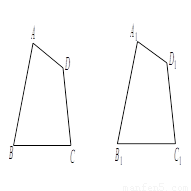
(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形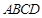 和四边形
和四边形 为例,分为以下四类:
为例,分为以下四类:
① ,
,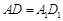 ,
,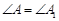 ,
,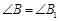 ,
,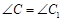 ;
;
②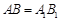 ,
,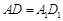 ,
,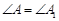 ,
,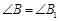 ,
,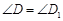 ;
;
③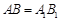 ,
,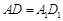 ,
,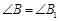 ,
,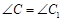 ,
,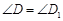 ;
;
④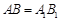 ,
,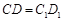 ,
,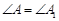 ,
,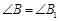 ,
,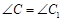 ;
;
其中能判定四边形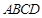 和四边形
和四边形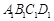 全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
科目:czsx 来源: 题型:解答题
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
【实践操作】如图.
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开,得到AD∥EF∥BC.
第二步:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM.折痕BM 与折痕EF相交于点P.连接线段BN,PA,得到PA=PB=PN.
【问题解决】
(1)求∠NBC的度数;
(2)通过以上折纸操作,还得到了哪些不同角度的角?请你至少再写出两个(除∠NBC的度数以外).
(3)你能继续折出15°大小的角了吗?说说你是怎么做的.
科目:czsx 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:解答题
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
【实践操作】如图.
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开,得到AD∥EF∥BC.
第二步:再一次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM.折痕BM 与折痕EF相交于点P.连接线段BN,PA,得到PA=PB=PN.
【问题解决】
(1)求∠NBC的度数;
(2)通过以上折纸操作,还得到了哪些不同角度的角?请你至少再写出两个(除∠NBC的度数以外).
(3)你能继续折出15°大小的角了吗?说说你是怎么做的.

科目:czsx 来源: 题型:阅读理解
【问题提出】
规定:四条边对应相等,四个角对应相等的两个四边形全等.
我们借助学习“三角形全等的判定”获得的经验与方法对“全等四边形的判定”进行探究.
【初步思考】
在两个![]() 四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
四边形中,我们把“一条边对应相等”或“一个角对应相等”称为一个条件,满足4个条件的两个四边形不一定全等,如边长相等的正方形与菱形就不一定全等.类似地,我们容易知道两个四边形全等至少需要5个条件.
【深入探究】
小莉所在学习小组进行了研究,她们认为5个条件可分为以下四种类型:
Ⅰ一条边和四个角对应相等;
Ⅱ二条边和三个角对应相等;
Ⅲ三条边和二个角对应相等;
Ⅳ四条边和一个角对应相等.
(1)小明认为“Ⅰ一条边和四个角对应相等”的两个四边![]() 形不一定全等,请你举例说明.
形不一定全等,请你举例说明.
(2)小红认为“Ⅳ四条边和一个角对应相等”的两个四边形全等,请你结合下图进行证明.
已知:如图, .
求证: .
证明:

(3)小刚认为还可以对“Ⅱ二条边和三个角对应相等”进一步分类,他以四边形![]() 和四边形
和四边形![]() 为例,分为以下四类:
为例,分为以下四类:
①![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
②![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
④![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
其中能判定四边形![]() 和四边形
和四边形![]() 全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
(4)小亮经过思考认为也可以对“Ⅲ三条边和二个角对应相等”进一步分类,请你仿照小刚的方法先进行分类,再概括得出一个全等四边形的判定方法.
科目:czsx 来源:2012年山东省青岛市李沧区中考数学一模试卷(解析版) 题型:解答题
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?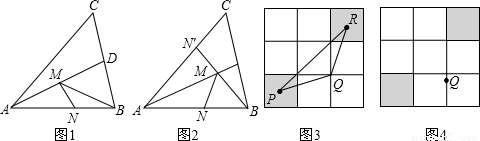
科目:czsx 来源:不详 题型:解答题

 和四边形
和四边形 为例,分为以下四类:
为例,分为以下四类: ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ;
; ,
, ,
, ,
, ,
, ;
; ,
,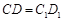 ,
, ,
, ,
, ;
; 和四边形
和四边形 全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .
全等的是 (填序号),概括可得“全等四边形的判定方法”,这个判定方法是 .