科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题
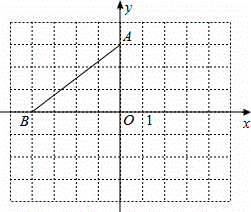 在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0),将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.科目:czsx 来源:安徽省淮南市潘集区2011-2012学年八年级第二次联考数学试题 题型:044
如图,在平面直角坐标系中点A(0,2),B(6,4)

(1)请你在x轴上找一点C,使它到点A、B的距离之和为最小,则点C的坐标为(________,________);
(2)在图中,作出ΔABC关于直线y轴的对称图形ΔA1B1C1;
(3)直接写出ΔA1B1C1三个顶点坐标.
科目:czsx 来源: 题型:
 在平面直角坐标系中,点A(0,2),B(6,4).
在平面直角坐标系中,点A(0,2),B(6,4).科目:czsx 来源: 题型:
 如图,在平面直角坐标系中点A(0,2),B(6,4)
如图,在平面直角坐标系中点A(0,2),B(6,4)科目:czsx 来源: 题型:解答题
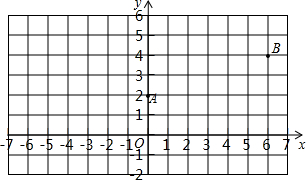 如图,在平面直角坐标系中点A(0,2),B(6,4)
如图,在平面直角坐标系中点A(0,2),B(6,4)科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:
 如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0.
如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0.| PA+PB |
| PC |
科目:czsx 来源: 题型:
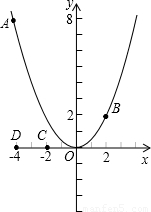
如图,已知点A(-4,8)和点B(2,n)在抛物线![]() 上.
上.
(1) 求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2) 平移抛物线![]() ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
① 当抛物线向左平移到某个位置时,A′C+CB′ 最短,求此时抛物线的函数解析式;
② 当抛物线向左或向右平移时,是否存在某个位置,使四边形A′B′CD的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
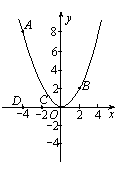
科目:czsx 来源: 题型:
 已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.
已知点A在数轴上对应的数为a,点B对应的数为b,A、B之间的距离记作AB,定义:AB=|a-b|,且|a+2|+(b-5)2=0.| v1 |
| v2 |
科目:czsx 来源:2009年浙江省舟山市初中毕业生学业考试数学试题卷、答案 题型:059
如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.
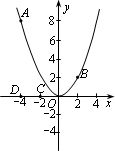
(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2,记平移后点A的对应点为![]() ,点B的对应点为
,点B的对应点为![]() ,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
①当抛物线向左平移到某个位置时,![]() 最短,求此时抛物线的函数解析式;
最短,求此时抛物线的函数解析式;
②当抛物线向左或向右平移时,是否存在某个位置,使四边形![]() 的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
科目:czsx 来源:2009年浙江省衢州市初中毕业生学业考试数学试题 题型:059
如图,已知点A(-4,8)和点B(2,n)在抛物线y=a2上.

(1)求a的值及点B关于x轴对称点P的坐标,并在x轴上找一点Q,使得AQ+QB最短,求出点Q的坐标;
(2)平移抛物线y=ax2,记平移后点A的对应点为![]() ,点B的对应点为
,点B的对应点为![]() ,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
,点C(-2,0)和点D(-4,0)是x轴上的两个定点.
①当抛物线向左平移到某个位置时,![]() +
+![]() 最短,求此时抛物线的函数解析式;
最短,求此时抛物线的函数解析式;
②当抛物线向左或向右平移时,是否存在某个位置,使四边形![]() 的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
的周长最短?若存在,求出此时抛物线的函数解析式;若不存在,请说明理由.
科目:czsx 来源: 题型:
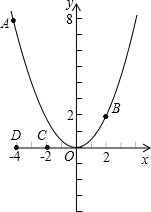 如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.
如图,已知点A(-4,8)和点B(2,n)在抛物线y=ax2上.科目:czsx 来源:浙江省中考真题 题型:解答题

 ,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点。
,记平移后点A的对应点为A′,点B的对应点为B′,点C(-2,0)和点D(-4,0)是x轴上的两个定点。科目:czsx 来源:第2章《二次函数》中考题集(30):2.7 最大面积是多少(解析版) 题型:解答题

科目:czsx 来源:第34章《二次函数》中考题集(34):34.4 二次函数的应用(解析版) 题型:解答题

科目:czsx 来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版) 题型:解答题

科目:czsx 来源:第6章《二次函数》中考题集(33):6.4 二次函数的应用(解析版) 题型:解答题