科目：czsx 来源： 题型：
科目：czsx 来源：2012-2013学年北京市西城区（北区）八年级上学期期末考试数学试卷（带解析） 题型：解答题
在△ABC中，AD是△ABC的角平分线．
（1）如图1，过C作CE∥AD交BA延长线于点E，若F为CE的中点，连结AF，求证：AF⊥AD；
（2）如图2，M为BC的中点，过M作MN∥AD交AC于点N，若AB=4， AC=7，
求NC的长．
科目：czsx 来源：2012-2013学年北京市西城区（北区）八年级上学期期末考试数学试卷（解析版） 题型：解答题
在△ABC中，AD是△ABC的角平分线．
（1）如图1，过C作CE∥AD交BA延长线于点E，若F为CE的中点，连结AF，求证：AF⊥AD；
（2）如图2，M为BC的中点，过M作MN∥AD交AC于点N，若AB=4， AC=7，
求NC的长．
科目：czsx 来源： 题型：解答题
科目：czsx 来源：不详 题型：解答题
科目：czsx 来源： 题型：解答题
科目：czsx 来源： 题型：
在Rt△ACB中，∠ACB=90°，BD是∠ABC的角平分线，交AC于点D，CE⊥AB于点E，交BD于点O，过O点作FG∥AB，交BC于点F，交AC于点G．科目：czsx 来源： 题型：解答题
在Rt△ACB中，∠ACB=90°，BD是∠ABC的角平分线，交AC于点D，CE⊥AB于点E，交BD于点O，过O点作FG∥AB，交BC于点F，交AC于点G．科目：czsx 来源：不详 题型：解答题
科目：czsx 来源：2016届江苏省兴化市七年级下学期期中考试数学试卷（解析版） 题型：解答题
如图①，△ABC的角平分线BD、CE相交于点P.
（1）如果∠A=70°，求∠BPC的度数；
（2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求∠MPB+∠NPC的度数（用含∠A的代数式表示）；
① ② ③ ④
在（2）的条件下，将直线MN绕点P旋转.
（ⅰ）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，试探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；
（ⅱ）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的延长线上时，如图④，试问（ⅰ）中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由.
科目：czsx 来源： 题型：
科目：czsx 来源： 题型：
如图①，△ABC的角平分线BD、CE相交于点P.
（1）如果∠A=70°，求∠BPC的度数；
（2）如图②，过P点作直线MN∥BC，分别交AB和AC于点M和N，试求
∠MPB+∠NPC的度数（用含∠A的代数式表示）；
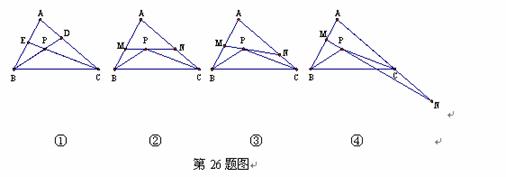
（3）在（2）的条件下，将直线MN绕点P旋转.
（i）当直线MN与AB、AC的交点仍分别在线段AB和AC上时，如图③，
试
探索∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由；
（ii）当直线MN与AB的交点仍在线段AB上，而与AC的交点在AC的
延长线上时，如图④，试问（i）中∠MPB、∠NPC、∠A三者之间
的数量关系是否仍然成立？若成立，请说明你的理由；若不成立，请
给出∠MPB、∠NPC、∠A三者之间的数量关系，并说明你的理由.
科目：czsx 来源： 题型：解答题
科目：czsx 来源： 题型：
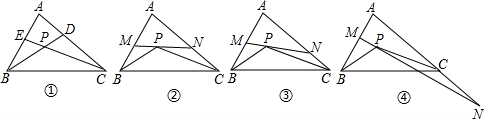
如图,等腰直角 △ABC 中, AC=BC,∠ACB =900, AF 为△ABC的角平分线,分别过点 C, B 作 AF 的垂线,垂足分别为 E ,D.以下结论:① CE=DE=
;② AF= 2BD ;③ CE+ EF=
;④
.其中结论正确的序号是( )
（A）①②③ （B）①②④ （C）①③④ （D）②③④
科目：czsx 来源： 题型：
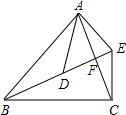如图，在△ABC中，BA=BC，过C点作CE⊥BC交∠ABC的角平分线BE于点E，连接AE，D是BE上的一点，且∠BAD=∠CAE．科目：czsx 来源： 题型：
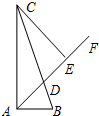在直角三角形ABC中，∠CAB=90°，∠ABC=72°，AD是∠CAB的角平分线，交边BC于点D，过点C作△ACD中AD边上的高线CE，则∠ECD的度数为（ ）科目：czsx 来源： 题型：单选题
在直角三角形ABC中，∠CAB=90°，∠ABC=72°，AD是∠CAB的角平分线，交边BC于点D，过点C作△ACD中AD边上的高线CE，则∠ECD的度数为
如图，CE是△ABC的角平分线，过点E画BC的平行线，交AC于点D，交外角∠ACG的平分线于点F．试证明DE=DF．
23、如图，CE是△ABC的角平分线，过点E画BC的平行线，交AC于点D，交外角∠ACG的平分线于点F．试证明DE=DF．
如图，已知AD是△ABC的角平分线，求证：